Телеконтроль и телеуправление в энергосистемах - Коды Хэмминга Телеконтроль и телеуправление в энергосистемах

Страница 22 из 46

Коды Хэмминга предназначены для исправления и обнаружения всех однократных ошибок (при d = 3), исправления однократных ошибок и обнаружения двукратных (при d = 4) и т. д.

Все n разрядов кода под разделяются на информационные и контрольные (проверочные): n=nи+ к. Число рабочих комбинаций . Число контрольных разрядов находится из выражения

(3.16)

В табл. 3.13 приведены значения л и для различных к, удовлетворяющих выражению (3.16).

Таблица 3.13. Числа контрольных к и информационных nи разрядов в -разрядном коде Хэмминга (d = 3)

Контрольные символы осуществляют дополнение до четности (либо нечетности) числа единиц в определенной группе символов в кодовой комбинации. Значения контрольных символов однозначно определяются значениями информационных символов в контролируемой группе (в соответствии с так называемыми проверочными уравнениями) .

Число контрольных символов, равное числу проверок на четность определенных групп символов, должно быть таким, чтобы в результате проверок могла быть сформирована кодовая комбинация, однозначно указывающая на номера искаженных символов в принятой последовательности и символов (включая и контрольные символы).

Контрольные символы в принципе могут располагаться в любых местах -разрядного кода: после информационных символов, либо до них, либо вперемежку с ними. Однако для большего удобства проверки принятого кода контрольные символы располагаются в разрядах, кратных степени двойки, т. е. под контрольные символы отводятся 1-й, 2-й, 4-й, 8-й и т. д. разряды. Остальные разряды заполняются информационными символами.

Так, например, для кода Хэмминга G (12,8) информационные символы располагаются в 12, И, 10, 9, 7, 6, 5-м и 3-м разрядах. Каждый контрольный символ осуществляет дополнение до четности (либо нечетности) числа единиц в контролируемой группе символов. Разделение символов на к контрольных производится следующим образом. Номера разрядов «-разрядного кода записываются в виде двоичных чисел. Например, для кода G (12,8) (n = 12, nи=8, к =4) имеем

В первую контрольную группу входят те разряды, двоичный номер которых содержит 1 в первом разряде, т. е. 13, 5,7,9,11.

Во вторую контрольную группу входят разряды, двоичный номер

которых содержит 1 во втором разряде: 2, 3, 6, 7, 10, 11 и т. д. Число 1 в контрольных группах должно быть четным. Отсюда значения контрольных разрядов хi, i=1, 2, 4, 8, находятся из следующих проверочных уравнений:

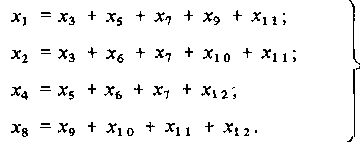(3.17)

Ниже приведена образующая матрица кода Хэмминга G (12,8). Информационные символы образуют единичную подматрицу I8, контрольные, определенные в соответствии с проверочными уравнениями (3.17), образующую подматрицу G'(4,8):

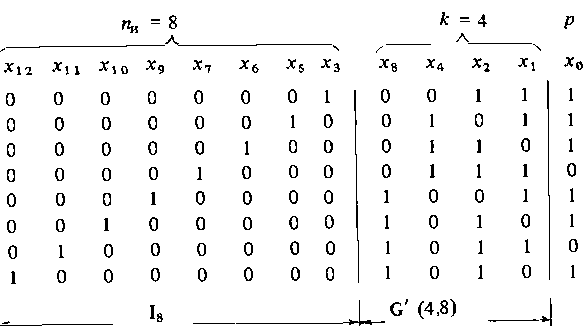
(3.18)

При кодировании принятых кодовых комбинаций осуществляется проверка четности единиц в контрольных группах, сформированных передающим устройством. В результате этих проверок декодер формирует двоичное число, однозначно указывающее на номер разряда, в котором произошла ошибка. Это число называют опознавателем ошибок. Поскольку код Хэмминга при d=3 способен исправлять только однократные ошибки, опознавателем может служить двоичное число, обозначающее номер разряда кодовой комбинации. Число разрядов опознавателя при этом совпадает с числом контрольных разрядов к. Формируется опознаватель следующим образом: если в проверяемой контрольной группе четность сохранилась, то в соответствующий разряд опознавателя записывается 0, если не сохранилась, — 1. Образованное в результате к проверок двоичное число укажет номер искаженного разряда, который при декодировании должен быть заменен на инверсный. В этом состоит исправляющая способность кода.

Для примера положим, что при посылке кодовой комбинации, соответствующей 4-й строчке кода G (12,8), в информационном символе х5 произошла ошибка: вместо 0 была принята 1. Тогда проверка декодером первой контрольной группы (разряды 1, 3, 5, 7, 9, 11) зафиксирует 1, второй контрольной группы — 0, третьей — 1, четвертой — 0.

Таким образом, будет сформирован опознаватель 0101 — двоичное число 5, указывающее на необходимость инверсии х5. Тем самым исправляется однократная ошибка.

Двукратные ошибки в коде Хэмминга при d=3 могут только обнаруживаться, но не исправляться. Для обнаружения ошибок достаточно, чтобы опознаватель отличался от нуля, что указывает на наличие однократной или двукратной ошибки. Однако такой опознаватель не будет опознавать номеров разрядов, в которых произошли ошибки, т. е. код не может исправлять однократные и двукратные ошибки.

Расширенный код Хэмминга (d = 4) обеспечивает исправление всех однократных и обнаружение всех двукратных ошибок (r= 2, s = 1). Он образуется добавлением проверки четности единиц во всех разрядах кода (дополнительный проверочный разряд х0 в образующей матрице) . Тем самым достигается увеличение кодового расстояния до 4.

Декодирование расширенного кода Хэмминга.

Возможны следующие ситуации при приеме кодовой комбинации:

все контрольные группы фиксируют 0 — при этом приемник фиксирует отсутствие ошибок и дает разрешение на воспроизведение принятой кодовой комбинации;
общая проверка на четность фиксирует 1, в остальных контрольных группах формируется опознаватель искажения, не равный 0, — приемник фиксирует однократную ошибку, которую следует исправить по сформированному опознавателю;
общая проверка на четность фиксирует 0, в остальных контрольных группах набирается опознаватель, не равный 0, — приемник фиксирует двукратную ошибку, которую следует не исправлять, а лишь констатировать ее наличие при приеме.

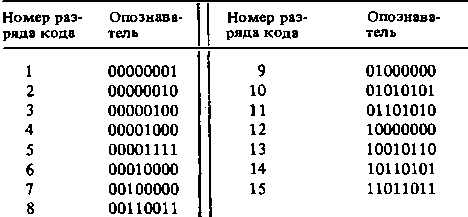
Таблица 3.14. Опознаватели однократных ошибок для кодов, исправляющих однократные и двукратные ошибки

Исправление ошибок кратности s > 2

Для кодов, исправляющих двукратные ошибки и ошибки большей кратности, построение опознавателей более сложно, так как вид опознавателя должен однозначно указывать на одновременные ошибки в s разрядах в различных сочетаниях С. Поэтому опознаватели для исправления s > 2 ошибок берутся из специальных таблиц, полученных с помощью вычислительных машин. В частности, в [19] приведены таблицы опознавателей для s = 2 и 3 вплоть до 29-го разряда. В табл. 3.14 приведены опознаватели однократных ошибок для кодов, исправляющих все двукратные ошибки (s=2) вплоть до 15-го разряда. Опознаватели двукратных ошибок, например в i -м и j-м разрядах, могут быть получены из этой таблицы путем суммирования по модулю 2 опознавателей однократных ошибок в i-м и j-м разрядах. Так, например, опознавателем двукратной ошибки во 2-м и 5-м разрядах будет вектор 00001101.

Составление проверочных уравнений по опознавателям.

Число разрядов опознавателя равно числу проверок на четность, т. е. числу контрольных символов к. Согласно табл. 3.14 15-разрядный код, исправляющий все двукратные ошибки (s = 2), должен иметь к = 8 контрольных разрядов. Следовательно, число информационных разрядов = = 7. Номера контрольных разрядов определяются по таблице опознавателей: они соответствуют тем разрядам, опознаватели которых имеют по одной 1. Из табл. 3.14 находим, что контрольные символы располагаются в 1,2, 3, 4, 6, 7, 9-м и 12-м разрядах. Из нее же следует, что появление 1 в первом разряде опознавателя может явиться результатом ошибок в 1, 5, 8, 10, 14-м и 15-м разрядах. Появление 1 во втором разряде опознавателя может явиться следствием ошибок во 2, 5, 8, 11, 13-м и 15-м разрядах и т. д. Отсюда проверочные уравнения для кода G (15,7) будут следующие:

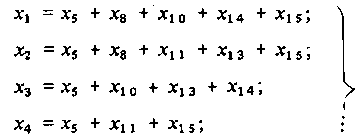(3-19)

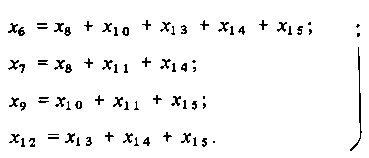
Зная закон определения проверочных символов, нетрудно записать любую из 27 = 128 комбинаций кода G (15,7) путем записи номера комбинации двоичным числовым кодом, разряды которого размещаются в 5, 8, 10, 11,13, 14-м и 15-м разрядах, а в остальных разрядах размещаются проверочные символы в соответствии с уравнениями (3.19).