Телеконтроль и телеуправление в энергосистемах - Коды с обнаружением и исправлением ошибок Телеконтроль и телеуправление в энергосистемах

Страница 21 из 46

Коды с обнаружением r-кратных и исправлением s-кратных ошибок должны обладать минимальным кодовым расстоянием, определяемым условиями (3.3) и (3.4). Увеличение кодового расстояния достигается увеличением числа разрядов кода п при уменьшении числа используемых рабочих комбинаций Nр, т. е. увеличением Киз.

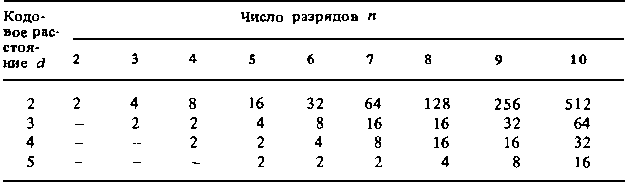
В табл. 3.12 приведено количество рабочих комбинаций с кодовым расстоянием d в зависимости от числа разрядов в коде п для d < 5 и и < 10 [10]. Из таблицы следует, что с увеличением d резко снижается число используемых (рабочих) комбинаций, так, при d = 5 (при этом код способен обнаруживать и исправлять двукратные ошибки) и n=10 число рабочих комбинаций N =16 из 210 = 1024 возможных комбинаций двоичного без избыточного кода.

Предельное число рабочих комбинаций, удовлетворяющих условию исправления всех ошибок кратности до s включительно, согласно Хэммингу составляет

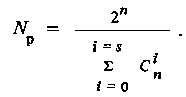(3.15)

Практически этот теоретический предел достигается далеко не всегда. В частности, данные табл. 3.12 несколько занижают число Nр по сравнению с (3.15). Однако, изменяя исходные комбинации, с которыми производится сравнение всех остальных, можно получить данные, более близкие к (3.15).

Таблица 3.12. Количество рабочих комбинаций Nр с кодовым расстоянием d и числом разрядов п

Определение рабочих комбинаций, обладающих заданным кодовым расстоянием, из общего числа N = 2” двоичного без избыточного кода является основной задачей теории кодирования. Известно множество способов решения этой задачи, которые предлагают различные коды, обнаруживающие и исправляющие ошибки. Применительно к телемеханике наибольшее распространение получили так называемые разделимые групповые систематические коды [16].

Разделимые систематические групповые коды

Все символы разделимых кодов разделяются на информационные символы и контрольные (проверочные) к: п = пи+ к.

Значения контрольных символов находятся по определенной системе в результате проведения некоторых линейных алгебраических операций над информационными символами. Поэтому такие коды получили название разделимых систематических кодов или просто систематических.

Все двоичные систематические коды являются групповыми кодами, поскольку они удовлетворяют условию существования алгебраической конечной группы относительно операции сложения по модулю 2.

Сокращенное обозначение группового кода G (п, пи), где п — общее число разрядов кода; — число информационных разрядов.

Набор рабочих кодовых слов определяется числом информационных разрядов:

Число проверочных символов в кодовом слове и способ их формирования определяются тем, какие и сколько ошибок должен исправлять или обнаруживать данный код.

Значения проверочных символов для каждой рабочей комбинации

определяются однозначно по информационным символам. Правила нахождения контрольных символов по информационным, обеспечивающие заданное минимальное кодовое расстояние, и определяют разнообразие разделимых групповых кодов.

Для определения всех комбинаций группового линейного кода достаточно определить контрольные символы только для единичных векторов информационной части кода, число которых равно пи. Совокупность информационных и контрольных символов для единичных информационных векторов, записанная в виде матрицы, образует так называемую образующую матрицу, содержащую пи строк и (пи + к) столбцов:

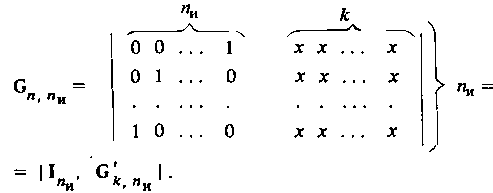
Величины х в подматрице принимают значения 1 или 0 в зависимости от правил формирования кода. Подматрицаназывается дополняющей образующей подматрицей. Поскольку единичная подматрица I всегда детерминирована, все многообразие кодовых и комбинаций кода G(n, nи) определяет подматрица

По образующей матрице определяются все рабочие комбинации искомого кода. Для этого необходимо произвести сложение по модулю 2 строк образующей матрицы во всех сочетаниях.

Ниже рассматриваются два класса разделимых групповых кодов, получивших преимущественное распространение в телемеханике.