Телеконтроль и телеуправление в энергосистемах - Основные характеристики кодов Телеконтроль и телеуправление в энергосистемах

Страница 18 из 46

Число используемых символов (или букв в кодовом алфавите) определяет основание кода т. По значению т коды подразделяются на двузначные (двоичные, бинарные) при т=2, трехзначные (т = 3) и многозначные (т>3). Число разрядов п в кодовых комбинациях определяет длину кода. Если длина всех кодовых слов одинакова (п = const), то код называется равномерным.

Емкость кода — число комбинаций (кодовых слов) из общего числа N = тn используемых для передачи сообщений. Эти комбинации называются рабочими Np. Закон Np=f(n,m), по которому составляются рабочие комбинации, и является кодом.

Избыточность кода, коэффициент избыточности.

Из всех возможных кодовых комбинаций N=тn для передачи сообщений используется лишь некоторая часть (Np< N). Остальные же избыточные комбинации служат для целей проверки правильности прохождения кодированного сигнала. Если вместо посланной кодовой комбинации принята кодовая комбинация, не входящая в число Np, то это означает, что в процессе передачи произошла ошибка.

Принятая искаженная комбинация анализируется. Результатом анализа может явиться сигнал ошибки (защитное действие) либо восстановление посланного сигнала (исправление ошибки). Таким образом, способность кодов обнаруживать (или исправлять) ошибки связана с их избыточностью. Избыточность кодов характеризуется коэффициентом избыточности

(3.1)

Значение Kиз лежит в пределах 0 < Киз < 1. Код, у которого используются все возможные комбинации в качестве рабочих (Np = N), называется без избыточным непомехозащищенным кодом. Для такого кода Киз =0.

Кодовое расстояние d между двумя кодовыми комбинациями (кодовыми векторами) равно числу одноименных разрядов с отличными символами. Для двузначных кодов кодовое расстояние определяется как вес (т. е. число единиц) суммы по модулю 2 двух кодовых комбинаций. Например, d между комбинациями 0110111 и 1101010 равно 5, поскольку сумма по модулю 2 1011101 имеет вес, равный 5.

Кодовое расстояние играет важную роль при рассмотрении помехозащищенности кодов. Оно характеризует, насколько одна рабочая комбинация удалена от другой. Чем больше d, тем труднее при прочих равных условиях помехам исказить посланную комбинацию так, чтобы она превратилась в другую рабочую комбинацию, т. е. чтобы было принято ложное сообщение.

Таблица 3.1. Матрица кодовых расстояний d. .

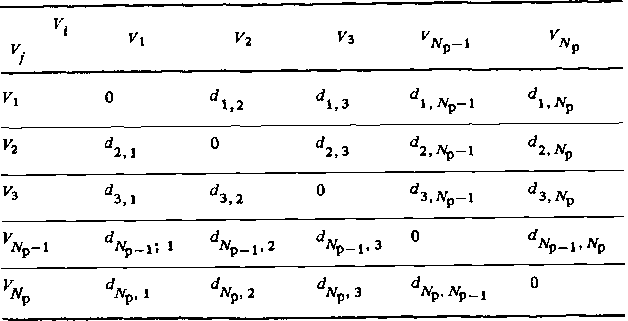
В теории помехозащищенных кодов помехи характеризуются кратностью помех, указывающей число символов кода, которые помеха способна исказить (в двузначных кодах 0 заменить 1 и наоборот). Так, однократная помеха искажает один разряд кодовой комбинации, двукратная — два и т. д.

Если вероятность однократной помехи обозначить р, то для симметричного двоичного канала без памяти вероятность двукратной помехи составит р2, трехкратной -р3 и т. д. Ясно, что при такой модели канала наибольшую опасность имеют однократные помехи, поскольку они наиболее вероятны.

Для характеристики помехозащищенности кода в целом существует понятие минимального кодового расстояния d . - минимально-

го расстояния между любыми парами кодовых векторов, входящих в данный код.

Совокупность кодовых расстояний между всеми рабочими векторами кода Nр образует матрицу кодовых расстояний (табл. 3.1). Минимальное кодовое расстояние определяется из этой матрицы:

Величина dmin характеризует минимальную кратность помехи, которая может привести к не обнаруживаемым ошибкам (т. е. к приему ложных сообщений). Так, при dmin = 1 уже однократная помеха, т. е. помеха, искажающая всего один бит в кодовой комбинации, приводит к ложному сообщению. Следует подчеркнуть, что в избыточных кодах не все искажения кратности dmin вызывают ложные сообщения.

Однако dmin характеризует ту наименьшую кратность помехи, которая достаточна для появления ложных сообщений.

Зависимость между кодовым расстоянием и кратностью обнаруживаемых и исправляемых ошибок.

Чем большим кодовым расстоянием обладает код, тем он имеет большую потенциальную помехозащищенность. Для обнаружения всех ошибок кратности до r минимальное кодовое расстояние должно быть равно

dmin=r+i· (3-2)

Выполнение условия (3.2) означает, что любая помеха кратности до r не сможет перевести одну рабочую комбинацию в другую, т. е. не сможет образовать ложного сообщения, а переводит рабочую комбинацию в область запрещенных, которые приемник может просто обнаружить и запретить их исполнение.

Существуют коды, которые позволяют не только обнаруживать ошибки, но и исправлять их и тем самым восстанавливать исходные кодовые комбинации, искаженные при передаче. Для исправления ошибок кратности s минимальное кодовое расстояние должно быть увеличено по сравнению с расстоянием, определяемым по формуле (3-2):

(3-3)

При этом кодовые комбинации с ошибками кратности до s как бы группируются вокруг соответствующей рабочей комбинации, образуя группу кодовых векторов, удаленных от данной рабочей комбинации на меньшие расстояния, чем от любых других. Это обстоятельство и используется для исправления ошибок кратности не более s: принятая кодовая комбинация расшифровывается как рабочая, если отстоит от рабочей на расстоянии, не превышающем s.

Для исправления s-кратных и обнаружения r-кратных ошибок необходимо выполнение следующего условия:

(3.4) причем r > s.

Коды, позволяющие обнаруживать (исправлять) ошибки, называются также корректирующими (самокорректирующими).

Таблица 3.2. Распределение кодовых векторов d по кодовым расстояниям А.

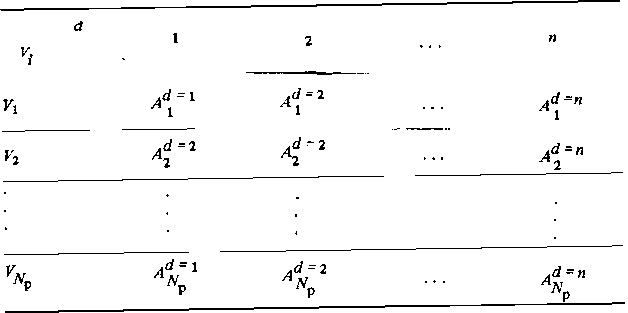
Распределение рабочих кодовых комбинаций по кодовым расстояниям.

Матрица кодовых расстояний (табл. 3.1) позволяет определить для всех рабочих векторов Vi, i = 1, 2, . . ., Np, числа кодовых векторов, удаленных от данного на расстояния d = 1,2, . . ., п. Эти числа А представляют собой распределение i -го рабочего вектора по кодовым расстояниям в ансамбле рабочих кодов (табл. 3.2). Минимальное значение d в этом распределении равно dmin, максимальное может достигать числа разрядов п (если все разряды кодовых комбинаций инверсны). Если все кодовые векторы имеют одинаковое распределение кодовых расстояний

то такой код является симметричным. Для характеристики симметричного кода, очевидно, достаточно иметь распределениедля одного любого кодового вектора.

Распределение кодовых векторов по кодовым расстояниям позволяет более детально (по сравнению с известной величиной dmin) охарактеризовать потенциальную помехозащищенность кода. Зная это распределение, можно определить, от какого количества ошибок той или иной кратности защищен данный код. Для этого необходимо вычислить коэффициенты не обнаруживаемых (ложных) переходов одной рабочей комбинации в другие под влиянием помех заданной кратности.

Для простейших кодов существуют формулы для вычисления

Однако в общем случае эти вычисления производятся с помощью несложных программ на ЭВМ.

Коэффициент ложных переходов определяется следующим образом:

(3.5)

где

— число рабочих векторов, отстоящих от данного рабочего

вектора на расстоянии d;— суммарное число возможных кодовых векторов той же разрядности п, отстоящих от данного рабочего вектора на расстоянии d.

Величинадля всех двузначных кодов определяется числом сочетаний из числа разрядов n по d:

Рабочий вектор под воздействием d-кратной помехи может перейти в множествовекторов, причем если он попадет в подмножество

этого множества, то будет принято ложное сообщение. Коэффициенти характеризует долю ложных переходов под влиянием d-кратной помехи.

Для симметричных кодов, как было отмечено, существует единое распределение .для кода в целом. Поэтому подсчетдля таких кодов производится непосредственно по выражению (3.5).

Для несимметричных кодов можно определить лишь среднее значение, для чего определяетсядля каждого из Np векторов в отдельности (i=1,2,..., Np) и затем производится усреднение по всем рабочим кодовым векторам:

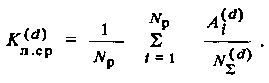(3.6)