Телеконтроль и телеуправление в энергосистемах - Числовые коды Телеконтроль и телеуправление в энергосистемах

Страница 19 из 46

Алфавитом кодовых комбинаций могут служить цифры. Составив из цифр число и сопоставив это число с определенным сообщением, получим числовой код этого сообщения.

Системы счисления

Целое число N может быть записано в любой системе счисления в виде ряда

(3-7) где т — основание системы счисления; п — количество разрядов числа; z — номер разряда; кi — разрядные коэффициенты.

Основание т системы счисления определяет ее название: т = 2 — двоичная система, т = 3 — троичная и т. д.

Наиболее распространены следующие системы счисления, используемые при формировании числовых кодов в машинных системах: двоичная, восьмеричная, шестнадцатеричная. Для записи чисел в двоичной системе используются всего две цифры: 0 и 1. В восьмеричной системе числа изображаются с помощью восьми цифр: 0, 1,2, 3, 4, 5, 6, 7, В шестнадцатеричной системе требуется шестнадцать знаков, в качестве которых используются десять цифр от 0 до 9 и шесть букв А, В, С, D, Е, F (табл. 3.3).

Для наиболее распространенной в обычной практике вычислений десятичной системы т = 10, к; = 0-9. В ней число, например, 249 записывается в виде ряда

(3.7) следующим образом:

Обычно принятая форма записи числа основана на записи лишь разрядных коэффициентов.

Аналогично для двоичной системы

Таблица 3.3. Запись чисел в различных системах счисления
Десятичные	Двоичные	Восьмеричные	Шестнадцатеричные
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	12	9
10	1010	12	А
11	1011	14	В
12	1100	14	С
13	1101	15	D
14	1110	16	Е
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
32	100000	40	20
64	1000000	100	40
100	1100100	144	64
128	10000000	200	80
256	100000000	400	100

для восьмеричной системы

для шестнадцатеричной системы

Количество кодовых комбинаций числового кода равно =тп. Чем выше основание системы счисления, тем меньшее число разрядов имеет заданное число , т. е. тем короче кодовая комбинация (так, из приведенных примеров видно, что для записи одного и того же числа 249 в шестнадцатеричной системе требуется два разряда, в десятичной и восьмеричной — три, в двоичной — восемь).

Наименование числовых кодов определяется системой счисления, положенной в основу их формирования.

Числовой двоичный код

Все N сообщений нумеруются порядковой последовательностью в двоичной системе счисления, образующей двоичный код этих сообщений. Двоичная система имеет ряд преимуществ, особенно в условиях машинного счета. Наличие в этой системе всего двух знаков (О и 1) как нельзя лучше соответствует двум позициям двухпозиционных элементов (триггеров), используемых в различных автоматических устройствах. Исключительное распространение, которое получила двоичная система в современной вычислительной технике, объясняется также чрезвычайной простотой арифметических действий в этой системе.

Количество кодовых комбинаций двоичного кода равно

Следовательно, для записи в двоичном коде данного числа сообщений N требуется иметь разрядов:

где- ближайшее большее целое число.

В двоичном коде используются все возможные кодовые комбинации, т. е. = . Поэтому этот код является неизбыточным и согласно (3.1) Киз=0.

Благодаря отсутствию избыточности двоичный код в принципе является непомехозащищенным; любая, даже однократная ошибка образует ложную комбинацию. Минимальное кодовое расстояние dmin = 1. Нетрудно показать, что коэффициент ложных переходов равен 1 для любого d.

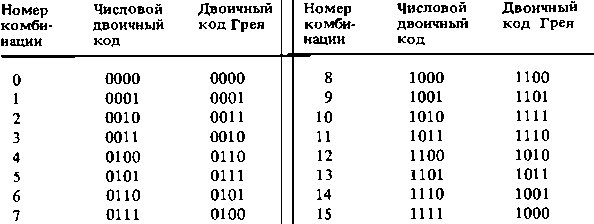
Таблица 3.4. Запись десятичных чисел (0-15) числовым двоичным кодом и кодом Грея

Благодаря простоте реализации двоичные коды широко используются на практике для формирования информационной части кода. Для придания кодовым комбинациям большей помехозащищенности к информационным символам добавляются защитные символы, которые и определяют помехозащищенность кода.

В качестве простейшей защиты двоичных кодов от искажений используется фиксация нарушения количества элементов в кодовой комбинации. Для этой цели в телемеханике всегда используются равномерные двоичные коды, т. е. такие, у которых все кодовые комбинации имеют одинаковую длину.

Другие виды защиты двоичного кода будут рассмотрены ниже.

Двоичный код Грея.

В кодоимпульсных телеизмерительных устройствах, в которых используется преобразование угла поворота в код, применяется специальный двоичный код, получивший наименование кода Грея. Отличительной, особенностью этого кода является то, что соседние кодовые комбинации, расположенные в порядке возрастания номеров, отличаются лишь в одном разряде. В простом двоичном коде это правило не соблюдается: например, при переходе от комбинации № 3 к № 4 единицы меняются во всех трех разрядах, от № 7 к № 8 — во всех четырех и т. д. Двоичный код Грея (первые 16 комбинаций) представлен в табл. 3.4.

Комбинации этого кода образуются из соответствующей комбинации простого двоичного кода путем суммирования ее по модулю 2 с этой же комбинацией, но сдвинутой на один разряд вправо. При этом младший разряд суммы отбрасывается.

Преимущество применения кода Грея состоит в том, что при преобразовании аналоговой величины (угла поворота, механического перемещения и т. п.) в код, например с помощью кодовой маски, погрешность преобразования не превышает погрешности дискретности, т. е. единицы младшего разряда, так как при переходе от одного уровня дискретности к другому меняется единица только в одном разряде. При применении же простого двоичного кода ошибка в фиксации старшего разряда на границе двух дискретных уровней приводит к ошибке равной 50% шкалы измерения.

Обратное преобразование кода Грея в двоичный код производится, начиная со старшего разряда, по следующему правилу. Сначала переписывается без изменения старший разряд преобразуемой комбинации. Значение каждого последующего разряда двоичного кода находится путем сложения по модулю 2 этого разряда в коде Грея с предыдущими, более старшими разрядами. Например, комбинация кода Грея 1001 соответствует следующей комбинации двоичного кода: старший разряд 1, следующий разряд 0 + 1 =1,0 + 0+ 1= 1, 1 +0 + 0+ 1 =0, т. е. 1110.

Код Грея является без избыточным (Киз =0, dvin =1), поэтому в принципе это не помехозащищенный код. Однако если допустить, что каждое последующее сообщение отличается от предыдущего не более чем на ± 1 (такие сообщения, например, характерны для циклических телеизмерений медленно меняющихся процессов), то закономерность кода Грея (отличие каждой соседней комбинации не более чем в одном разряде) может служить основой выявления ошибок в принятом сообщении: комбинация считается принятой правильно, если она отличается от предшествующей не более чем одним разрядом, все другие комбинации бракуются. При таких условиях код Грея можно считать помехозащищенным от всех ошибок кратности более 1.

Двоичный без избыточный код с кодовым расстоянием d> 2 между соседними кодовыми комбинациями.

Идею построения без избыточных кодов с кодовым расстоянием d > 1 между соседними кодовыми комбинациями предложил профессор Г. М. Бутаев, который разработал синтез и анализ этих кодов вплоть до d < 5 [21]. Эти коды целесообразно использовать для циклических телеизмерений медленно- меняющихся параметров. Рассмотрим без избыточный код с кодовым расстоянием d > 2 между соседними кодовыми комбинациями.

Этот код может быть синтезирован из двоичного числового кода по правилу, подобному синтезу кода Грея, с той лишь разницей, что комбинация этого кода образуется из исходной комбинации двоичного кода путем суммирования ее по модулю 2 со сдвинутой влево на один разряд этой же комбинацией. При этом отбрасывается старший разряд полученной суммы. Дополнительным правилом является следующее: если результатом суммирования по сформулированному выше правилу окажется исходная комбинация, то она инвертируется. В табл. 3.5 приведены комбинации описываемого кода для и = 4 и и = 5.

Таблица 3.5. Двоичный код с d > 2 между соседними кодовыми комбинациями

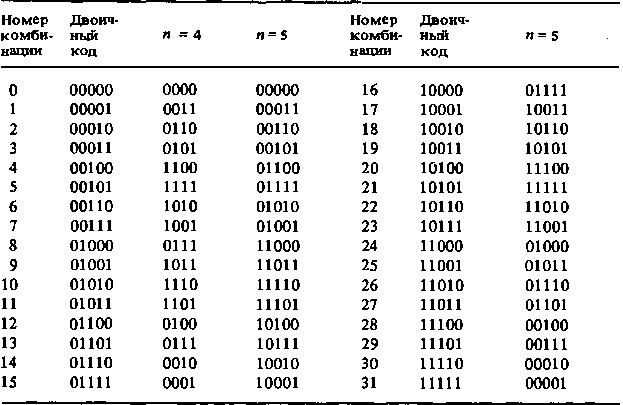
Комбинация № 8 для п = 4 и № 16 для п = 5 образованы инвертированием полученной комбинации (в соответствии с дополнительным правилом) . Расстояние между всеми соседними комбинациями равно двум за исключением комбинаций № 8 (для и =4) и № 16 (n=5), для которых оно равно трем.

Обратное преобразование в двоичный код производится, начиная с младшего разряда преобразуемой комбинации, по следующему правилу.

Сначала переписывается без изменения младший разряд. Значение каждого последующего (более старшего) разряда двоичного кода находится путем суммирования по модулю 2 этого разряда преобразуемого кода с предыдущими (более младшими) разрядами. Например, кобинация № 25 пятиразрядного без избыточного двоичного кода с d > 2 между соседними комбинациями 01011 соответствует следующей комбинации двоичного кода: младший (нулевой) разряд 1, первый разряд 1 + 1=0, второй 0 + 1 + 1 = 0, третий 1 + 0 + 1 + + 1 = 1, четвертый 0+1+0+1 + 1, т. е. 11001. Исключение в обратном переводе составляют, естественно, лишь комбинации № 8 (для л = 4) и № 16 (для n=5), которые образуются в результате их обратного инвертирования. В общем случае n-разрядного кода номера инвертируемых комбинаций соответствуют числам 2n-1.

Минимальное кодовое расстояние в рассматриваемом коде dmin= 1, так что в принципе он допускает ложные сообщения при однократных ошибках (например, переход комбинаций № 11 в № 21, № 13 в№21,№15в№31 и др.). Однако если ввести ограничения на передаваемые сообщения, заключающиеся в том, что с вероятностью, близкой к 1, каждое последующее сообщение отличается от предыдущего не более чем на ± 1 квант, то описанный без избыточный код обнаруживает все однократные ошибки, т. е. обладает свойствами помехозащищенного кода с d = 2. При этом приемник должен лишь контролировать, что принятая комбинация отличается от предшествующей не более чем на ± 1 (т. е. разрешенная апертура приема Н = 2). В случае выхода принятой комбинации за разрешенную апертуру она бракуется.

Двоично-десятичные коды базируются на двоично-десятичной системе счисления. Каждый разряд десятичного числа записывается в виде двоичного четырехразрядного числа (тетрады). Поскольку тетрадой можно записать 16 различных цифр, десятичная цифра может бьггь записана различными двоичными числами. Это порождает многообразие двоично-десятичных кодов.

Все двоично-десятичные коды подразделяются на весовые и невесовые. ’’Весом” единицы разряда двоичного числа является ее эквивалент в десятичной системе. Сумма весов двоичной тетрады равна цифре десятичного числа. Весовым двоично-десятичным кодом называется такой код, в котором веса разрядов для всех десяти комбинаций сохраняются постоянными.

В табл. 3.6 представлены некоторые весовые двоично-десятичные коды, отличающиеся весом разрядов двоичного числа.

Перечисление весов разрядов дает название двоично-десятичному коду, например: код 8-4-2-1, код 5-4-2-1, код 2-4-2-1 и т. д.

Код 8—4—2—1 является единственным весовым кодом, в котором разрядные коэффициенты десятичного числа могут быть получены однозначно: например, цифре 6 соответствуют единицы в первом и втором разрядах; цифре 9 — в нулевом и третьем разрядах и т. д. Поэтому код 8-4-2-1 очень удобен для преобразователей типа код- аналог, применяемых в приемниках кодоимпульсных телеизмерительных устройств. Наличие единицы в соответствующем разряде однозначно может быть отображено добавлением соответствующей порции (веса) аналоговой величины (например, выходного тока или напряжения) на выходе преобразователя.

Код 5-4—2-1, как видно из табл. 3.6, обладает той интересной особенностью, что вторая половина кодовых комбинаций (5-9) во всех разрядах, кроме старшего, повторяет кодовые комбинации первой половины (0-4) и лишь в старшем разряде нуль заменяется единицей.

Код 2-4-2-1 может быть получен инверсным отображением кодовых комбинаций относительно центральной оси, делящей все комбинации на две равные части.

Таблица 3.6. Весовые двоично-десятичные коды

Выбор того или иного двоично-десятичного кода диктуется целым рядом конкретных условий его использования и соображениями удобства его реализации.

Двоично-десятичные коды широко применяются при построении дискретных телеизмерительных систем, особенно в тех случаях, когда измеряемый параметр должен воспроизводиться на цифровых указывающих приборах.

Двоично-десятичные коды обладают некоторой избыточностью — коэффициент избыточности в каждой декаде примерно равен 0,2. Это обстоятельство может быть использовано для обнаружения некоторых ошибок. Для этой цели кроме десяти рабочих комбинаций должны фиксироваться и остальные шесть комбинаций, причем при приеме этих комбинаций, которые могут быть лишь результатом ошибок при передаче кода, должен обеспечиваться запрет воспроизведения информации. Однако при этом обнаруживаются далеко не все, даже самые простые, однократные ошибки.

Двоично-шестнадцатеричный код широко используется для сокращенной записи кодовых комбинаций, имеющих байтную структуру. Двоичное четырехразрядное число записывается шестнадцатеричным символом (см. табл. 3.3). При этом двоичный байт (8 разрядов двоичного кода) записывается шестнадцатеричными разрядами. Например, двоичные последовательности 1110 0111, 1011 1101 записываются соответственно Е7 и BD. Точка перед символами* отличает двоичношестнадцатеричные двухразрядные числа от двухразрядных шестнадцатеричных чисел (7)16 = (231)10 и (BD)16 = (189)10.

* В литературе встречается также обозначение ”Н” вместо точки: Е7Н, BDH и т. д.