Принцип наложения (суперпозиции)

Каждая ЭДС в уравнении ( 1.49) представляет собой алгебраическую сумму ЭДС во всех ветвях контура I. Если в (1.49) заменить все контурные ЭДС алгебраическими суммами ЭДС ветвей, то после группировки слагаемых получится выражение для контурного тока в виде алгебраической суммы составляющих токов, вызванных каждой из ЭДС ветвей в отдельности, при этом каждая составляющая тока равна произведению ЭДС ветви на алгебраическую сумму коэффициентов, входящих в ( 1.49).

Это чрезвычайно важное свойство называется принципом наложения и непосредственно следует из линейности уравнений, описывающих режим цепей с линейными элементами.

Принцип наложения справедлив не только для контурных токов , но и для токов ветвей, так как систему независимых контуров можно всегда выбрать так, что рассматриваемая ветвь войдет только в один контур, т. е. контурный ток , будет равен току в ветви.

В качестве примера, иллюстрирующего принцип наложения, рассмотрим электрическую схему, показанную на рис. 2.1, для которой, пользуясь методом контурных токов, запишем следующие уравнения: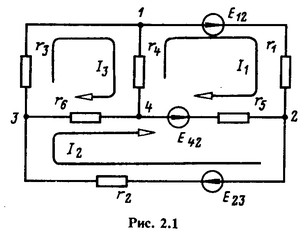

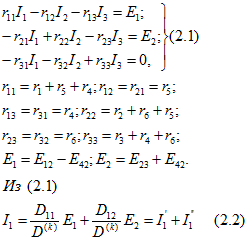
где

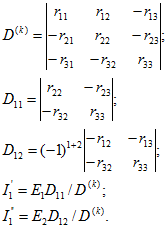
Дополнительно по теме

Аналогично определяются токи I1 и I2

Если в (2.2) контурные ЭДС заменить ЭДС в ветвях, то получим

откуда и следует, что контурный ток I1 равен алгебраической сумме составляющих токов, вызываемых каждой из ЭДС в отдельности. Кроме того, этот контурный ток равен току ветви с сопротивлением r1 и ЭДС Е12, так как по этой ветви другие контурные токи не замыкаются.

Таким образом, при определении токов ветвей при помощи принципа наложения можно поочередно оставлять в схеме по одной ЭДС, считая все остальные ЭДС источников равными нулю, но сохраняя в схеме их внутренние сопротивления. Ток ветви равен алгебраической сумме токов, вызываемых каждой ЭДС. Если схема содержит не только источники ЭДС, но и источники тока, то следует найти составляющие токов ветвей, вызываемые каждым источником ЭДС и каждым источником тока, после чего определить токи ветвей путем алгебраического суммирования этих составляющих.

Так как принцип наложения следует из общих свойств линейных уравнений, то его можно применять для определения любых физических величин, которые связаны между собой линейной зависимостью. В применении к электрическим цепям можно определять не только токи при заданных сопротивлениях, ЭДС и токах источников, но и напряжения при заданных токах и известных сопротивлениях. Однако этим принципом нельзя пользоваться для вычисления мощностей, так как мощность - квадратичная функция тока или напряжения. Например, мощность в сопротивлении r1 (рис. 2.1) определяется по формуле

Если мощность того же элемента с сопротивлением r1 можно было бы считать равной сумме мощностей, обусловленных частичными токами то получилось бы совсем другое значение:

Пример 2.1.

На рис. 2.2, а показана мостовая схема с источником ЭДС Е = 5 В и источником тока J = 1 А. Сопротивления элементов указаны на схеме. Пользуясь принципом наложения, определить токи во всех ветвях.

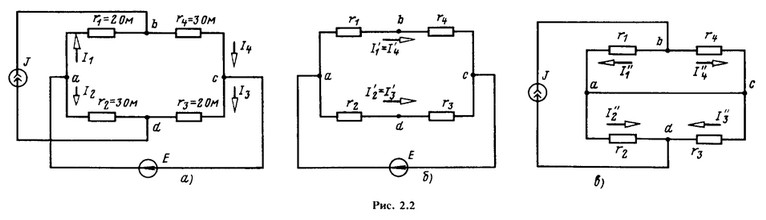
Решение.

Для определения токов в ветвях с применением принципа наложения надо рассчитать токи в двух схемах, изображенных на рис. 2.2,б и е. В схеме рис. 2.2, б J = 0 (точки b и d разомкнуты), а в схеме рис. 2.2, в Е = 0 (точки а и с соединены проводником без сопротивления). Токи в ветвях схемы (рис. 2.2,6)

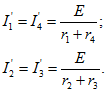
Токи в ветвях схемы по рис. 2.2, в, где сопротивления r1 и r4, а также r2 и r3 соединены параллельно,

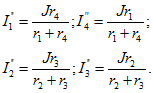
Токи в ветвях заданной схемы (рис. 2.2, а) равны алгебраическим суммам токов в соответствующих ветвях схем рис. 2.2,6 и в:

Анологично

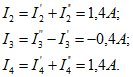
Смотри ещё по теме Электрические цепи постоянного тока

Основные законы и методы расчета электрических цепей постоянного тока

Основные свойства электрических цепей постоянного тока