Метод контурных токов

Для расчета режима сложной электрической цепи можно ограничиться совместным решением лишь К = (В - У + 1) независимых уравнений, составленных на основании второго закона Кирхгофа методом контурных токов; здесь В, как и ранее,-число ветвей и У - число узлов, при этом первый закон Кирхгофа, конечно, всегда удовлетворяется.

Для иллюстрации применения метода контурных токов рассмотрим схему на рис. 1.21, а с шестью ветвями и четырьмя узлами. Прежде чем составлять уравнения по второму закону Кирхгофа, надо выбрать взаимно независимые контуры.

При выборе независимых контуров можно применять то же правило, что и при записи уравнений по второму закону Кирхгофа. Например, для схемы рис. 1.21, а ветви с токами I4, I5 и I6, соединяющие узлы 1, 2, 3, 4, можно выбрать в качестве ветвей дерева (рис. 1.21,6); поэтому ветви с токами 1и 12 и 73 будут ветвями связи. На рис. 1.21,6 элементы ветвей дерева изображены сплошными линиями, а элементы ветвей связи - штриховыми.

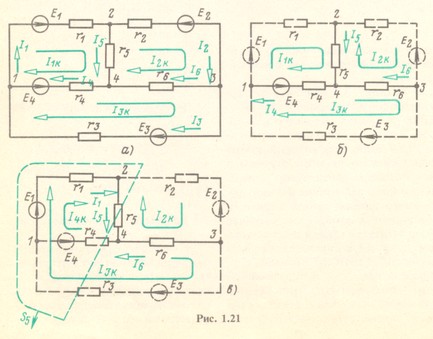
Для схем на рис. 1.21, а и б по первому закону Кирхгофа

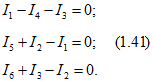
На основании второго закона Кирхгофа для трех контуров, каждый из которых включает только одну ветвь связи,

Дополнительно по теме

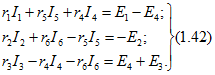
Пользуясь уравнениями (1.41), исключим из уравнений (1.42) токи /4, /5 и /6 всех ветвей дерева, общих для нескольких контуров; в результате получим

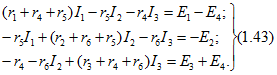
В соответствии с уравнениями (1.43) можно принять, что каждый из токов I1и I2 и I3 замыкается через соответствующую ветвь связи в одном из контуров (рис. 1.21, а и б), и назвать такие токи контурными: Напряжения на резистивных элементах любого контура равны алгебраической сумме напряжений, обусловленных токами своего и смежных контуров. Например, в контуре из элементов r1, r5 и r4 разность ЭДС E1 - Е4 равняется сумме трех напряжений: от собственного контурного тока I1к на всех сопротивлениях этого контура и от токов I2к и IЗк соответственно на сопротивлениях r5 и r4. Токи в ветвях дерева, общих для нескольких контуров, равны алгебраическим суммам контурных токов:

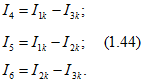
Для этой же схемы можно получить и другие взаимно независимые уравнения. Например, выберем другое дерево из первой, пятой и шестой ветвей (рис. 1.21, в), так что вторая, третья и четвертая ветви будут ветвями связи, токи в которых совпадают с контурными. Применив в этом случае второй закон Кирхгофа для контуров 2-3-4-2, 3-1-2-4-3 и 2-4-1-2, получим уравнения с контурными токами I2к, I3к и I4к, замыкающимися через ветви деревьев по ветвям связи. Токи в ветвях дерева однозначно определяются через токи ветвей связи (совпадающие с контурными) по формулам

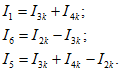
Выражение для тока I5 получено по первому закону Кирхгофа для токов в ветвях, примененному к главному сечению S5, след которого показан на рис. 1.21, в штриховой линией.

Таким образом, система взаимно не-зависимых уравнений определяется структурой выбранного дерева и соответствующими ветвями связи.

Схема рис. 1.21, а имеет 16 деревьев, поэтому для такой схемы можно написать 16 систем независимых уравнений, каждая из которых содержит в качестве неизвестных три тока, замыкающихся по ветвям связи через ветви выбранного дерева.

Из приведенных примеров следует, что для определения токов в ветвях этим методом нужно ввести в расчет контурные токи и решить совместно систему уравнений, составленных по второму закону Кирхгофа; число этих уравнений меньше числа неизвестных токов ветвей В на число узлов схемы без одного (У - 1). При замене токов в ветвях контурными токами первый закон Кирхгофа удовлетворяется для каждого узла, так как каждый контурный ток в одной из ветвей контура направлен к узлу, а в другой - от того же узла. Например, для узла 4 (рис. 1.21, а) по первому закону Кирхгофа для токов ветвей получим: , или для контурных токов .

Если схема содержит не только источники ЭДС, но и источники тока, то можно принять ток каждого из источников тока замыкающимся по любым ветвям дерева, составляющим с ветвью источника тока - ветвью связи - замкнутый контур. Падение напряжения, вызванное током такого источника на каждом из сопротивлений контура, учитывается при записи левой части уравнений по второму закону Кирхгофа. Эти напряжения можно также учесть с обратным знаком в правой части уравнений.

В качестве примера рассмотрим схему на рис. 1.17. На основании второго закона Кирхгофа

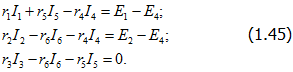
Пользуясь первым законом Кирхгофа, исключим из этих уравнений токи I5, I4 и I6; в результате после группировки слагаемых получим

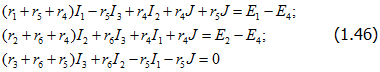
Из этих уравнений следует, что в рассматриваемом случае ток J как бы замыкается по ветвям с сопротивлениями r5 и r4, дополняющими ветвь с источником тока J до замкнутого контура.

Обозначив в уравнениях (1.46) составляющие напряжений r4J и r5J соответственно через Eт4 и Ет5, можно переписать их иначе:

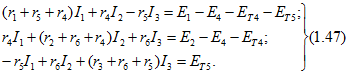
Здесь следует отметить, что перенос слагаемых r4J и r5J из левой в правую часть уравнений (1.47) и замена этих напряжений на схеме ЭДС Ет4 и Ет5 иллюстрируют применение так называемого принципа компенсации, изложенного более подробно в разделе.

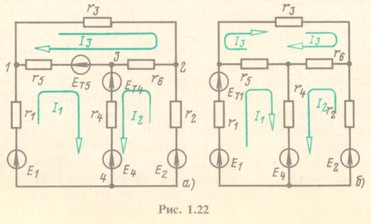
Уравнениям (1.47) соответствует эквивалентная схема (рис. 1.22, а), на которой источник тока J заменен источниками ЭДС Ет4 = r4J и Ет5 = r5J, при этом токи в ветвях с сопротивлениями г4 и г5 не равны соответствующим токам в ветвях заданной схемы (см. рис. 1.17) и отличаются от них на ток J источника тока. Иначе говоря, после определения контурных токов I1к, I2к и I3к необходимо для вычисления токов I4 и I5 в ветвях заданной схемы (рис. 1.17) записать уравнения по первому закону Кирхгофа именно для заданной схемы:

Аналогично можно показать, что если принять ток J замыкающимся по ветви с сопротивлением r1, то получится новая эквивалентная схема (рис. 1.22, 6); контурный ток I1к в эквивалентной схеме не равен току I1 в ветви с сопротивлением r1 заданной схемы (см.рис. 1.17) и отличается от него на ток J.

Замена источника тока J двумя эквивалентными источниками напряжения Ет4 и Ет5 (рис. 1.22, а) основана на предварительном преобразовании одного источника тока, включенного к узлам 1 и 4 (см. рис. 1.17) двумя источниками тока, включенными к узлам 1 и 3, 3 и 4. Покажем справедливость такого преобразования для более общего случая.

На рис. 1.23, а изображена часть разветвленной схемы с одним источником тока J, присоединенным к узлам 1 и 4. Режим в этой схеме, очевидно, не изменится, если вместо одного источника тока J, присоединенного к выводам / и 4, включить три источника тока соответственно к узлам 1 и 2, 2 и 3, 3 и 4, поскольку токи . в ветвях присоединения к узлам 2 и 2', 3 и 3' равны нулю (рис. 1.23,6). Переход от схемы рис. 1.23, б к эквивалентной схеме рис. 1.23,в, где уже не требует особых пояснений.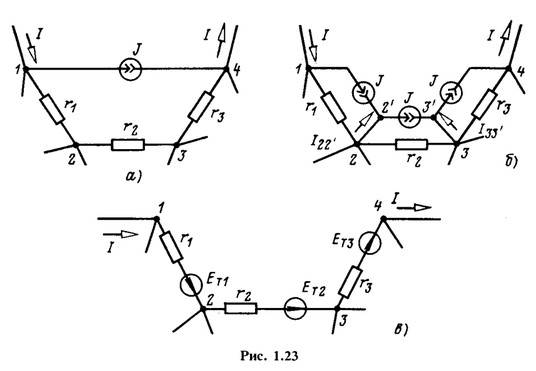

Таким образом, при расчете режима цепи методом контурных токов можно предварительно заменить источники тока эквивалентными источниками ЭДС, а затем ввести контурные токи и на основании второго закона Кирхгофа составить систему уравнений для их определения. Токи в ветвях без эквивалентных источников ЭДС, заменяющих источники тока, определяются по первому закону Кирхгофа суммированием контурных токов; в ветвях заданной схемы, в которых на эквивалентной схеме включены источники ЭДС, учитываются и токи источников тока.

При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки (на рис. 1.21,а три ячейки с контурными токами I1к, I2к и I3к), руководствуясь указанным выше правилом выбора независимых контуров (дерева и ветвей связи) при составлении уравнений на основании второго закона Кирхгофа, что возможно для любой планарной схемы.

Положительные направления контурных токов можно выбирать и произвольно, т. е. независимо от положительных направлений токов в ветвях.

Установим теперь более общие, необходимые для дальнейших выводов соотношения между контурными токами, сопротивлениями и ЭДС цепи произвольной конфигурации.

Для схемы, имеющей К независимых контуров, уравнения, аналогичные (1.43), запишутся в виде

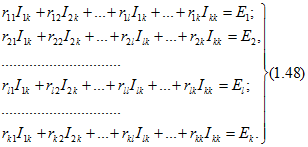
В этих уравнениях сопротивление вида ru (с двумя одинаковыми индексами) называется собственным сопротивлением контура l, а сопротивление вида (с двумя различными индексами) - общим сопротивлением контуров l и к. Правые части уравнений (1.48) называются контурными ЭДС. Каждая из контурных ЭДС вида Е1 равна алгебраической сумме ЭДС всех источников в ветвях контура l. Положительные знаки в каждом уравнении (1.48) должны быть взяты для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.

В более общем случае для электрической цепи, которая содержит как источники ЭДС, так и источники тока, контурное уравнение для l-го контура записывается в виде

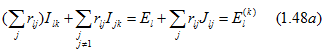
где обозначает собственное сопротивление контура l; - общее сопротивление двух контуров: l и j; - ток источника тока, замыкающийся по ветви с сопротивлением ; - контурная ЭДС (алгебраическая сумма ЭДС в контуре).

Решив систему уравнений (1.48) при помощи определителей относительно любого из токов, например , получим

где - определитель системы уравнений (1.48), т. е.

алгебраические дополнения определителя , причем получается из путем вычеркивания l-го столбца и q-й строки и умножения полученного определителя на .

Необходимо отметить, что сопротивления вида нужно записывать в выражении (1.50) с тем знаком, который стоит перед соответствующим напряжением в уравнениях (1.48).

Методом узловых потенциалов целесообразно пользоваться, если число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров У - 1 < К, а методом контурных токов - при У - 1 > К.

Матричные уравнения контурных токов.

Уравнения контурных токов (1.48) с учетом (1.48а) можно записать в матричной форме:

где - квадратная матрица контурных сопротивлений; - матрица-столбец контурных токов; - матрица-столбец контурных ЭДС, учитывающая источники ЭДС и эквивалентные ЭДС от источников тока.

После умножения уравнения (1.51) слева на получим

Покажем, что матрицу контурных сопротивлений можно получить непосредственно по схеме при помощи матрицы контуров В:

где r - диагональная матрица сопротивлений ветвей; - транспонированная матрица контуров.

Направление обхода каждого контура примем совпадающим с положительным направлением соответствующего контурного тока, а направления ветвей - с положительными направлениями токов в ветвях. Чтобы получить независимые контуры, следует сначала выбрать дерево схемы, что в свою очередь определяет ветви связи, а следовательно, и контурные токи.

Для иллюстрации рассмотрим схему на рис. 1.21, а с выбранным деревом из четвертой, пятой и шестой ветвей (рис. 1.21,6). В этом случае независимые контуры содержат контурные токи I1к, I2к и IЗк, что соответствует первой, второй и третьей ветвям связи.

Матрица контуров В состоит из трех строк и шести столбцов:

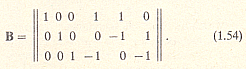
Диагональная матрица сопротивлений

Произведение матриц В и r равно:

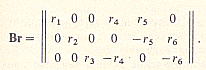
Квадратная матрица контурных сопротивлений определяется по (1.53):

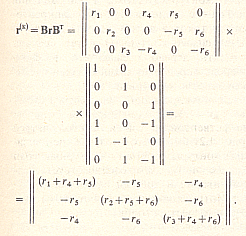
Матрица-столбец контурных токов

Матрица-столбец контурных ЭДС

Пользуясь уравнением (1.51), матрицами , можно получить уравнения (1.43).

Подчеркнем, что матрица токов ветвей I определяется через матрицу контурных токов по формуле

Например, для схемы рис. 1.21, а

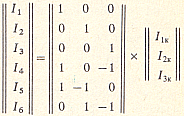
Из этого матричного уравнения сразу получаем равенства, определяющие токи ветвей через контурные токи:

В дальнейшем индекс "к" у контурных токов, как правило, будем опускать.

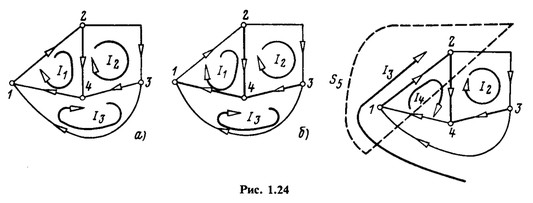
В заключение подчеркнем, что все соотношения между токами ветвей и контурными токами для схем, показанных на рис. 1.21, а -в, можно получить из графов, построенных соответственно для этих схем на рис. 1.24, а-в, при этом деревья графа изображены на рис. 1.24,6 и в толстыми линиями, а ветви связи - тонкими.

Смотри ещё по теме Электрические цепи постоянного тока

Основные законы и методы расчета электрических цепей постоянного тока

Основные свойства электрических цепей постоянного тока