Законы Кирхгофа и их применение

Для расчета разветвленной сложной электрической цепи существенное значение имеет число ветвей и узлов.

Ветвью электрической цепи и ее схемы называется участок, состоящий только из последовательно включенных источников ЭДС и приемников с одним и тем же током. Узлом цепи и схемы называется место или точка соединения трех и более ветвей (узлом иногда называют и точку соединения двух ветвей).

При обходе по соединенным в узлах ветвям можно получить замкнутый контур электрической цепи; каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза.

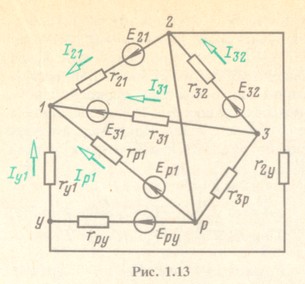
На рис. 1.13 в качестве примера показана схема электрической цепи с пятью узлами и девятью ветвями. В частных случаях встречаются ветви только с резистивными элементами без источников ЭДС (ветвь 1 - у) и с сопротивлениями, практически равными нулю (ветвь 2 - р). Так как напряжение между выводами ветви 2 - р равно нулю (сопро-тивление равно нулю), то потенциалы точек 2 и р одинаковы и оба узла можно объединить в один.

Режим электрической цепи произвольной конфигурации полностью определяется первым и вторым законами Кирхгофа.

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна пулю:

В этом уравнении одинаковые знаки должны быть взяты для токов, имеющих одинаковые положительные направления относительно узловой точки. В дальнейшем будем в уравнениях, составленных по первому закону Кирхгофа, записывать токи, направленные к узлу, с отрицательными знаками, а направленные от узла, - с положительными.

Если к данному узлу присоединен источник тока, то ток этого источника также должен быть учтен. В дальнейшем будет показано, что в ряде случаев целесообразно писать в одной части равенства (1.19а) алгебраическую сумму токов в ветвях, а в другой части алгебраическую сумму токов, обусловленных источниками токов:

где I - ток одной из ветвей, присоединенной к рассматриваемому узлу, a J - ток одного из источников тока, присоединенного к тому же самому узлу; этот ток входит в (1.196) с положительным знаком, если направлен к узлу, и с отрицательным, если направлен от узла.

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом контуре алгебраическая сумма напряжений на всех элементах и участках цепи, входящих в этот контур, равна нулю:

при этом положительные направления для напряжений на элементах и учасчках выбираются произвольно; в уравнении (1.20а) положительные знаки принимаются для тех напряжений, положительные направления которых совпадают с произвольно выбранным направлением обхода контура.

Дополнительно по теме

Часто применяется другая формулировка второго закона Кирхгофа: в любом замкнутом контуре алгебраическая сумма напряжений на всех участках с сопротивлениями, входящими в этот контур, равна алгебраической сумме ЭДС:

В этом уравнении положительные знаки принимаются для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.

В теории электрических цепей решаются задачи двух типов. К первому типу относятся задачи анализа электрических цепей, когда, например, известны конфигурация и элементы цепи, а требуется определить токи, напряжения и мощности тех или иных участков. Ко второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения на некоторых участках, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами синтеза электрических цепей. Отметим, что решение задач анализа намного проще решения задач синтеза.

В практической электротехнике довольно часто встречаются задачи анализа. Кроме того, для овладения приемами синтеза цепей необходимо предварительно изучить методы их анализа, которые преимущественно и будут в дальнейшем рассматриваться.

Задачи анализа могут быть решены при помощи законов Кирхгофа. Если известны параметры всех элементов цепи и ее конфигурация, а требуется определить токи, то при составлении уравнений по законам Кирхгофа рекомендуется придерживаться такой последовательности: сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнения для узлов на основании первого закона Кирхгофа и, наконец, составить уравнения для контуров на основании второго закона Кирхгофа.

Пусть электрическая цепь содержит В ветвей и У узлов. Покажем, что на основании первого и второго законов Кирхгофа можно составить соответственно У - 1 и В - У + 1 взаимно независимых уравнений, что в сумме дает необходимое и достаточное число уравнений для определения В токов (во всех ветвях).

На основании первого закона Кирхгофа для У узлов (рис. 1.13) можно написать У уравнений:

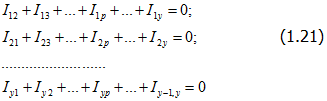
Так как любая ветвь связывает между собой только два узла, то ток каждой ветви должен обязательно войти в эти уравнения 2 раза, причем I12=-I21; I13=-I31 и т.д.

Следовательно, сумма левых частей всех У уравнений дает тождественно нуль. Иначе говоря, одно из У уравнений может быть получено как следствие остальных У - 1 уравнений или число взаимно независимых уравнений, составленных на основании первого закона Кирхгофа, равно У - 1, т. е. на единицу меньше числа узлов. Например, в случае цепи по рис. 1.14,о с четырьмя узлами

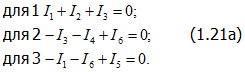
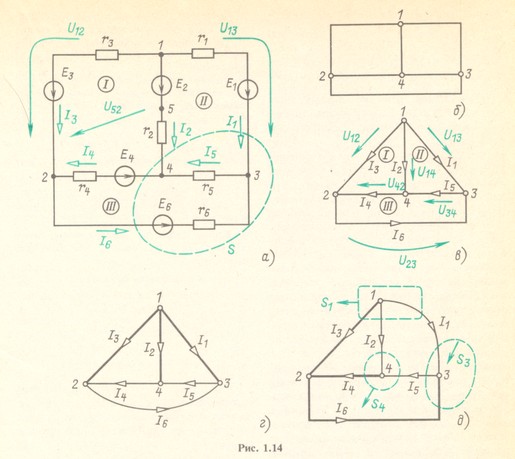
Добавим к этим У - 1 = 3 уравнениям уравнение

Суммируя четыре уравнения, получаем тождество 0 = 0; следовательно, из этих четырех уравнений любые три независимые, например первые три (1.21а).

Так как беспредельное накопление электрических зарядов не может происходить как в отдельных узлах электрической цепи, так и в любых ее частях, ограниченных замкнутыми поверхностями, то первый закон Кирхгофа можно применить не только к какому-либо узлу, но и к любой замкнутой поверхности - сечению.

Например, для поверхности S (рис. 1.14,а), как бы рассекающей электрическую схему на две части, справедливо уравнение , что можно также получить из уравнений (1.21) для узлов 3 и 4.

Чтобы установить число взаимно независимых уравнений, вытекающих из второго закона Кирхгофа, напишем для всех В ветвей схемы (рис. 1.13) В уравнений на основании закона Ома (1.11а):

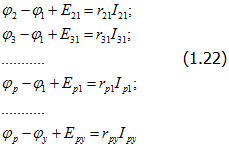
где - сопротивление ветви, со-единяющей узлы р и у; Еру - суммарная ЭДС, действующая в ветви р - у в направлении от р к у; - потенциалы узлов р и у.

В этих уравнениях суммарное число неизвестных токов В ветвей и потенциалов У узлов равняется В + У.

Не изменяя условий задачи, можно принять потенциал одного из узлов равным любому значению, в частности нулю. Если теперь из системы В уравнений (1.22) исключить оставшиеся неизвестными У - 1 потенциалов, то число уравнений уменьшится до В - (У - 1). Но исключение потенциалов из уравнений (1.22) приводит к уравнениям, связывающим ЭДС источников с напряжениями на резистивных элементах, т. е. к уравнениям, составленным на основании второго закона Кирхгофа.

Таким образом, число независимых уравнений, которые можно составить на основании второго закона Кирхгофа, равно В - (У- 1).

В качестве примера напишем уравнения, связывающие потенциалы узлов с токами и ЭДС для схемы рис. 1.14, а по ( 1.126):

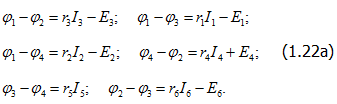
Сложив третье и четвертое уравнения и вычтя полученную сумму из первого, получим

Если применим второй закон Кирхгофа (1.206) к контуру 1-4-2-1 (при обходе вдоль контура по направлению движения часовой стрелки), то получим это же уравнение.

Аналогичным путем можно получить уравнения для других контуров:

для контура 1-3-2-1

для котуpa 2-4-3-2

Совместное решение любых пяти уравнений (1.21), (1.23) и (1.24) дает значения токов во всех ветвях электрической цепи, показанной на рис. 1.14, а. Если и результате решения этих уравнений получится отрицательное значение для какого-либо тока, то это значит, что действительное направление противоположно принятому за положительное.

При записи уравнений по второму закону Кирхгофа следует обращать особое внимание на то, чтобы составленные уравнения были взаимно независимыми. Контуры необходимо выбрать гак. чтобы в них вошли все ветви схемы, а в каждый из контуров - возможно меньшее число ветвей. Контуры взаимно независимы, если каждый последующий контур, для которого составляется уравнение, имеет не меньше одной новой ветви и не получается из контуров, для которых уже написаны уравнения, путем удаления из этих контуров общих ветвей. Например, контур 1-3-4-2-1 (рис. 1.14, а) можно получить из контуров 1-3-4-1 и 1-4-2-1 путем удаления ветви 1-4. Поэтому уравнение для контура 1-3-4-2-1 является следствием уравнений (1.23), (1.24а) и получается путем их суммирования. Далее будет дано наиболее общее правило выбора контуров, обеспечивающих получение независимых уравнений.

Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений (1.20) искомое напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения U52 (рис. 1.14, а) можно написать уравнение для контура 2-1-5-2

или для контура 5-4-2-5

откуда легко найти искомое напряжение.

Пример 1.2.

Пользуясь законами Кирхгофа, написать два выражения для тока I0 в ветви с гальванометром (рис. 1.15), приняв известным в одном случае ток I, а в другом напряжение U.

Решение.

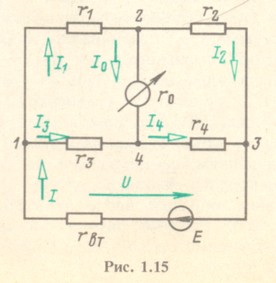
На основании законов Кирхгофа напишем для заданной схемы с шестью неизвестными токами уравнения:

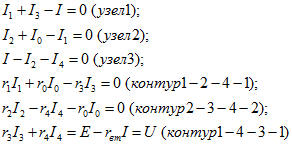
Решив совместно эти уравнения, получим выражения для тока I0 при заданном напряжении U

и при заданном токе I

Для полной характеристики электрического состояния цепи надо знать не только токи и напряжения, но также мощности источников и приемников энергии.

В соответствии с законом сохранения энергии развиваемая всеми источниками мощность равна суммарной мощности приемников и мощности потерь в источниках (из-за внутренних сопротивлений)

В левой части (1.25) суммы алгебраические. Это значит, что если при заданных направлениях действия источника ЭДС (см. рис. 1.7) или тока (см. рис. 1.8) для тока I в источнике ЭДС или напряжения U12 на выводах источника тока получится отрицательное численное значение, то этот источник в действительности не разовьет мощность, а получит ее от других источников. Соответствующее слагаемое в левой части (1.25) получится со знаком минус. Если требуется найти необходимую мощность источников питания цепи, то такие слагаемые следует записать с обратным знаком в правой части (1.25).

Смотри ещё по теме Электрические цепи постоянного тока

Основные законы и методы расчета электрических цепей постоянного тока

Основные свойства электрических цепей постоянного тока