Принцип эквивалентного генератора

Очень важным принципом эквивалентности, широко применяемым при анализе линейных электрических цепей, является принцип эквивалентного генератора (теорема об активном двухполюснике, или теорема Гельмгольца -Тевенена). Он формулируется следующим образом: любая линейная электрическая цепь, рассматриваемая относительно двух выводов (активный двухполюсник), эквивалентна реальному источнику с ЭДС, равной напряжению между этими выводами при размыкании внешнего участка цепи, подключенного к этим выводам (режим холостого хода). и внутренним сопротивлением, равным входному сопротивлению пассивного двухполюсника, получающегося при равенстве нулю всех ЭДС для источников ЭДС и токов для источников тока рассматриваемого двухполюсника. Применимость этого принципа к любой линейной электрической цепи доказывается на основании принципов компенсации и наложения.

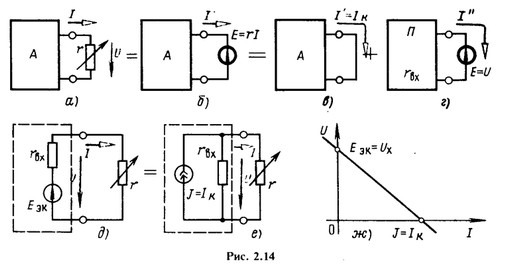
Пусть в электрической цепи выделен активный двухполюсник и ветвь с сопротивлением r (рис. 2.14, а), которое может быть и изменяющимся. Применив принцип компенсации, получим эквивалентную схему (рис. 2.14,6), для которой

E=U=rI (2.19)

Теперь применим принцип наложения и составим две схемы с двумя частными режимами: в первой из них (рис. 2.14, в) действуют только источники внутри активного двухполюсника, а ЭДС, полученная по принципу компенсации, полагается равной нулю, а во второй (рис. 2.14, г) действует только ЭДС компенсации (2.19), а двухполюсник считается пассивным. Его входное сопротивление .

Ток в ветви с сопротивлением r по принципу наложения равен сумме частичных токов , т. е. .

В частности, в режиме холостого хода I = 0 и . Следовательно

Последнее уравнение соответствует эквивалентной схеме, показанной на рис. 2.14, д с ЭДС , выражающей сформулированный выше принцип. Согласно (2.20) ток

Дополнительно по теме

Если источник ЭДС преобразовать в источник тока, то схема эквивалентного генератора получится такой, как на рис. 2.14, е. Вольт-амперная или внешняя характеристика эквивалентного генератора по рис. 2.14,6 или е показана на рис. 2.14, ж.

Следует заметить, что обе схемы эквивалентного генератора применимы только для расчета токов и напряжений в участке цепи, подключенном к рассматриваемому активному двухполюснику. Для мощностей, развиваемых источниками, и мощностей потерь внутри активного двухполюсника схемы замещения, полученные на основании принципа эквивалентного генератора, неадекватны.

Применение принципа эквивалентного генератора позволяет упростить решение многих задач, и поэтому его применение иногда относят к методам расчета, хотя он и носит более общий характер.

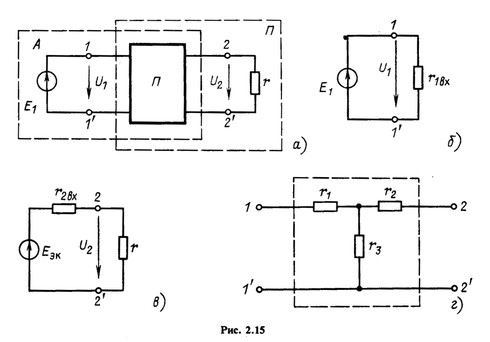
Применение принципа эквивалентного генератора весьма удобно при рассмотрении пассивного четырехполюсника, к одной паре выводов которого подключен источник ЭДС , а к другой паре выводов - приемник с сопротивлением r (рис. 2.15, а). Такую схему со стороны выводов 1-1' можно рассматривать как пассивный двухполюсник с сопротивлением (рис. 2.15,б), а со стороны выводов 2-2' - как активный двухполюсник с входным сопротивлением и ЭДС (рис. 2.15, в).

Если, например, пассивный четырехполюсник имеет схему, показанную на рис. 2.15, г, то параметры эквивалентной схемы

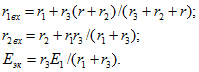
Представление четырехполюсника в виде эквивалентной схемы, изображенной на рис. 2.15, в, применяется при рассмотрении электронных схем. Для приемника с сопротивлениями r схемы рис. 2.15, а и в полностью эквивалентны. Однако если рассчитать мощность пассивного четырехполюсника (в сопротивлениях r1, r2 и r3) и мощность потерь в эквивалентной схеме (сопротивление rвх), то эти мощности могут оказаться равными только в редких частных случаях.

Интересно сопоставить принцип эквивалентного генератора с принципом компенсации. И тот и другой дают возможность представить двухполюсник в виде эквивалентного источника, однако принцип компенсации приводит к идеальному источнику ЭДС (без внутреннего сопротивления), а принцип эквивалентного генератора - к реальному источнику (с внутренним сопротивлением rвх). ЭДС источника, полученного на основании принципа компенсации, зависит от тока, а параметры источника, полученного на основании принципа эквивалентного генератора, не зависят от режима работы подключенного к активному двухполюснику участка цепи. Принцип компенсации применим как к линейным, так и к нелинейным цепям. Принцип эквивалентного генератора применим только к линейным цепям.

Пример 2.7.

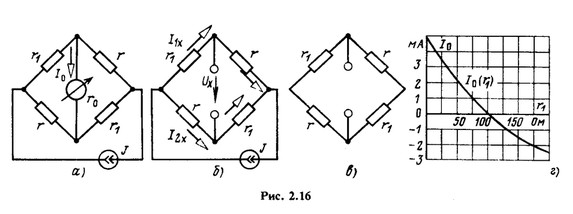
По принципу эквивалентного генератора найти выражение для тока в ветви с измерительным прибором (рис. 2.16, а), если ток источника тока J = 10 мА, сопротивление r = 100 Ом, сопротивление измерительного прибора r0 = 50 Ом, а сопротивления r1 двух противоположных плеч моста изменяются одновременно от нуля до 2r; построить график изменения тока I0 в зависимости от сопротивления r1.

Решение.

Разомкнем ветвь с измерительным прибором (рис. 2.16,6), отключив прибор, и найдем токи .

Напряжение (рис. 2.16,6) определим из уравнения , откуда .

Входное сопротивление двухполюсника относительно выводов ветви с измерительным прибором (рис. 2.16, в) .

По принципу эквивалентного генератора (2.21)

После подстановки в это выражение численных значений получим

На рис. 2.16, г показан график изменения тока I0 в зависимости от сопротивления r1. Из рисунка видно, что зависимость тока от сопротивления нелинейная (в отличие от линейных соотношений между ЭДС, напряжениями и токами при изменении сопротивления) и что при изменении сопротивления r1 изменяется не только значение тока I0, но и его направление.

Смотри ещё по теме Электрические цепи постоянного тока

Основные законы и методы расчета электрических цепей постоянного тока

Основные свойства электрических цепей постоянного тока