Теорема о взаимных приращениях токов и напряжений

Пользуясь ( 2.11) и (2.12), установим связь между приращениями токов и приращением напряжения при изменении сопротивления первой ветви в пределах от нуля до если (см. рис. 2.11).

Если , то напряжение и согласно (2.11) ток ; при сопротивлении первой ветви, равном , напряжение на ее выводах , а ток .

Следовательно, при изменении сопротивления первой ветви на изменение тока этой ветви

Аналогично можно показать, что при изменении сопротивления первой ветви на изменение тока во второй

Из (2.14) и (2.15) легко найти входную и взаимную проводимости ветвей через отношение приращений:

Согласно (2.12), где U1 при новых обозначениях надо заменить на получим

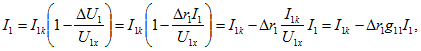
откуда

После подстановки этого выражения в (2.14) и (2.15) получаются формулы для определения приращений токов:

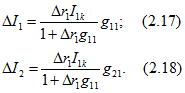
Выражения (2.17), (2.18) для приращений токов называют теоремой вариации или теоремой о взаимных приращениях. Если сопротивление первой ветви изменяется не от нуля до а от r1 до , то для определения приращений токов и можно пользоваться теми же формулами (2.17) и (2.18), при этом входная g11 и взаимная g21 проводимости, а также ток I1к имеют другие значения, определяемые, как и раньше, при

Смотри ещё по теме Электрические цепи постоянного тока

Основные законы и методы расчета электрических цепей постоянного тока

Основные свойства электрических цепей постоянного тока