Линейные соотношения между напряжениями и токами

В активном четырехполюснике с выводами 1-1' и 2-2' на рис. 2.11 кроме ветви с источником ЭДС Е1 выделена еще ветвь 2-2' с источником ЭДС Е2 и сопротивлением r2. Пользуясь принципом наложения, напишем выражение для токов I1 и I2 в ветвях схемы рис. 2.11, а в виде

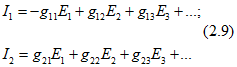
где ЭДС E3, E4 и т. д. находятся внутри четырехполюсника и знак минус перед проводимостью поставлен, так как положительное направление тока I1 противоположно направлению действия ЭДС Е1.

Предположим, что ЭДС первого источника Е1 может изменяться, а ЭДС остальных источников Е2, Е3 и т. д. неизменны. Так как входные () и взаимные () проводимости не зависят от значения ЭДС Е1, то, обозначив,

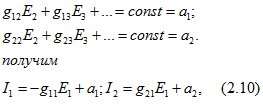
или, заменив в (2.10) ЭДС Е1 через U1,

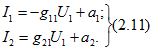
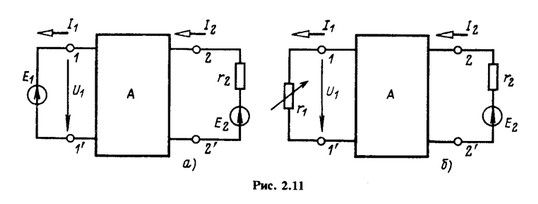
Как следует из принципа компенсации, изменение ЭДС E1, в схеме рис. 2.11, а равносильно изменению напряжения U1 при изменении сопротивления r1 в эквивалентной схеме рис. 2.11,6, при этом входная и взаимная проводимости не зависят от сопротивления r1, так как определяются для схемы рис. 2.11, а, где нет сопротивления r1.

Следовательно, при изменении сопротивления r1 токи I1 и I2 связаны с напряжением U1 линейными соотношениями.

Для определения постоянных расчетом или опытным путем необходимо, как следует из (2.11), рассчитать или измерить токи I1, I2 и напряжение U1 при двух режимах первой ветви (двух значениях сопротивления r1). Наиболее наглядно и просто эти постоянные определяются из режимов короткого замыкания (r1 = 0) и режима холостого хода ().

При коротком замыкании U1 = 0, токи

Дополнительно по теме

При размыкании первой ветви ток I1 = 0. Обозначив разность потенциалов между точками разрыва через U1x, а ток I1 = = I2х, получим согласно (2.11) в режиме холостого хода

откуда входная проводимость и взаимная проводимость

После замены постоянных в первом из уравнений (2.11) получается

Отметим, что изменение напряжения U1 в пределах от = 0 до U1 = U1x соответствует изменению сопротивления r1 от нуля до бесконечности.

Токи I1 и I2 рассматриваемых ветвей также связаны линейными соотношениями. Действительно, исключив из (2.11) напряжение U1, получим

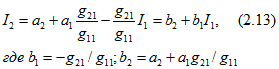
постоянные, которые определяются из двух любых режимов первой ветви или вычисляются при известных значениях входных и взаимных проводимостей.

Аналогично можно показать, что при одновременном изменении сопротивлений в двух ветвях напряжения и токи любых трех ветвей связаны линейным соотношением вида

z = а + bх + су,

где a, b и с - постоянные, определяемые опытным или расчетным путем; z, х и у - изменяющиеся токи или напряжения.

Пример 2.5.

На рис. 2.12, а изображена схема с резистором, сопротивление r которого изменяется от 0 до бесконечности. Найти зависимость тока в каждой ветви от напряжения U на выводах резистора с сопротивлением r, если и .

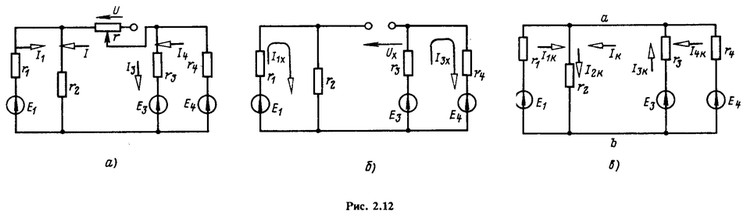
Решение.

Сначала найдем предельные значения напряжения U и тока I при коротком замыкании (r = 0) и холостом ходе () рассматриваемой ветви.

При ток Iх = 0, а напряжение U = Ux. Для схемы рис. 2.12, б , откуда .

Так как токи .

Для определения тока Iк (рис. 2.12, в) предварительно найдем напряжение на выводах параллельных ветвей по ( 1.34):

а затем токи в ветвях

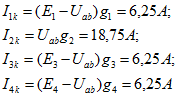
и ток

Зависимость тока i в резисторе от напряжения U на его выводах определяется линейным уравнением типа (2.11): I = а + + bU. Коэффициенты а и b найдем по результатам расчета режимов холостого хода и короткого замыкания. При r = 0 напряжение U = 0, а ток I = Iк = а = 12,5 А. При ток I = 0, напряжение U = Ux и 0 = Ik + bUх, откуда Ь = - Ik/Uх = - 12,5/50 = -0,25 См. В результате получаем I = 12,5-0,251U.

Зависимость тока I1 в первой ветви от напряжения U определяется уравнением прямой . Для того чтобы найти коэффициенты целесообразно и в этом случае пользоваться результатами расчета режимов холостого хода и короткого замыкания ветви с переменным сопротивлением r. При r = 0 напряжение U = 0, ток ; при (рис. 2.12, б) . Кроме того, , откуда . Следовательно, I1 = 6,25 + 0,1251U. Аналогично определяются токи I2 = 18,75 - 0,125U; I3 = I4 = 6,25 - 0,125U.

Пример 2.6.

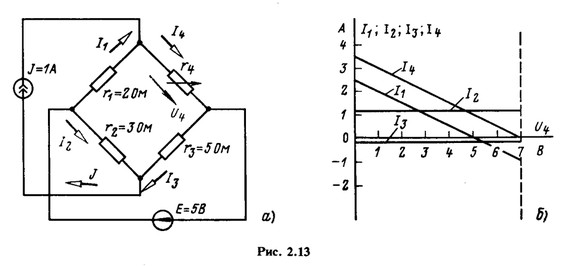
В схеме, показанной на рис. 2.13, а, сопротивление резистивного элемента изменяется в пределах от r4 = 0 (короткое замыкание) до (размыкание ветви). Пользуясь законами Кирхгофа, Выразить токи I1, I2, I3 и I4 через параметры схемы и напряжение U4 и построить найденные зависимости.

Решение.

Из уравнения непосредственно находим ток . Ток I4 определим по первому закону Кирхгофа:

Для определения токов I2 и I3 запишем уравнения Из этих уравнений находим токи

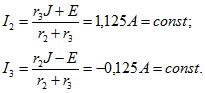
Оказалось, что токи I2 и I3 не зависят от сопротивления r4 (при любых его значениях остаются неизменными).

Для построения найденных зависимостей определим предельные значения напряжения U4 при изменении сопротивления r4. При r4 = 0 напряжения U4 = 0; при напряжение U4 = U4x. Это напряжение найдем из уравнения , откуда . Так как при (при размыкании ветви с сопротивлением r4) I1х = -J, то напряжение . Таким образом, при изменении сопротивления r4 от нуля до бесконечности напряжение U4 увеличивается от 0 до 7 В. На рис. 2.13,б показаны искомые зависимости.

Смотри ещё по теме Электрические цепи постоянного тока

Основные законы и методы расчета электрических цепей постоянного тока

Основные свойства электрических цепей постоянного тока