Преобразования в линейных электрических схемах
Преобразования в линейных электрических схемах
Расчет и исследование сложных электрических цепей во многих случаях можно значительно упростить и сделать более наглядными путем преобразования электрических схем одного вида в схемы другого вида. Целесообразное преобразование электрической схемы приводит к уменьшению числа ее ветвей или узлов, а следовательно, и числа уравнений, определяющих ее режим.
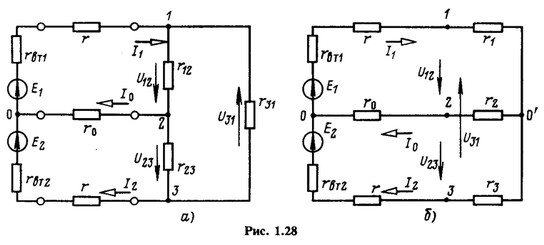
Рассмотрим, например, схему замещения трехпроводной линии (рис. 1.28, а). Пусть заданы ЭДС Е1, Е2 и внутренние сопротивления ![]() источников энергии, сопротивления проводов линии r, r0 и сопротивления приемников r12, r23 и r31.
источников энергии, сопротивления проводов линии r, r0 и сопротивления приемников r12, r23 и r31.
Для определения токов в шести ветвях этой схемы необходимо по методу контурных токов или узловых потенциалов решить систему уравнений с тремя неизвестными.
Однако можно упростить схему, например, так, чтобы она содержала только три ветви с тремя неизвестными токами и всего два узла. Новая схема получится, если три приемника с сопротивлениями r12, r23 и r31, присоединенных к узлам 1, 2 и 3, заменить тремя резистивными элементами с сопротивлениями r1, r2, r3 (рис. 1.28,6), включенными соответственно между точками 1, 2 и 3 заданной схемы и новой узловой точкой О'. После такой замены токи ![]() в ветвях, не затронутых преобразованием, и напряжения U12, U23 и U31 между точками 1, 2 и 3 должны быть такими же, как и в заданной схеме замещения.
в ветвях, не затронутых преобразованием, и напряжения U12, U23 и U31 между точками 1, 2 и 3 должны быть такими же, как и в заданной схеме замещения.
В новой, эквивалентной схеме с двумя узлами О и О' можно сразу найти напряжение между узловыми точками по формуле ( 1.34), а затем определить токи ![]() по закону Ома. После этого можно вычислить напряжения
по закону Ома. После этого можно вычислить напряжения ![]() между точками 1, 2 и 3 и токи I12, I23 и I31 в приемниках с сопротивлениями r12, r23 и r31 заданной схемы, т. е. решить задачу достаточно просто. Во всех случаях замены заданных электрических схем эквивалентными схемами другого вида необходимо выполнять условие неизменности токов и напряжений участков схемы, которые не затронуты преобразованиями.
между точками 1, 2 и 3 и токи I12, I23 и I31 в приемниках с сопротивлениями r12, r23 и r31 заданной схемы, т. е. решить задачу достаточно просто. Во всех случаях замены заданных электрических схем эквивалентными схемами другого вида необходимо выполнять условие неизменности токов и напряжений участков схемы, которые не затронуты преобразованиями.
Если преобразуется часть электрической схемы, не содержащая источников энергии, то, как будет видно из дальнейшего, неизменность токов и напряжений в остальной части схемы обеспечивает и неизменность мощностей элементов всех ветвей. В случае преобразования электрических схем, содержащих источники энергии, суммарные мощности источников и приемников в исходной схеме не равны в общем случае соответствующим мощностям в эквивалентной схеме.
Рассмотрим теперь наиболее характерные, чаще всего встречающиеся на практике случаи преобразования электрических схем как при отсутствии в преобразуемых ветвях источников ЭДС и тока, так и при их наличии.
Дополнительно по теме
- Элементы электрических цепей и схем
- Схемы замещения источников энергии
- Закон Ома для участка цепи с ЭДС
- Баланс мощностей для простой неразветвленной цепи
- Законы Кирхгофа и их применение
- Топологические графы
- Законы Кирхгофа в матричной форме
- Метод узловых потенциалов
- Метод контурных токов
- Уравнения цепи в матричной форме
- Расширенные узловые уравнения
- Преобразования в линейных электрических схемах
Преобразование соединения многолучевой звездой в соединение многоугольником; преобразование треугольника в
звезду.
Рассмотрим сначала преобразование соединения резистивных элементов (сопротивлений) многолучевой звездой (с числом лучей более трех) в эквивалентный многоугольник, т. е. преобразование пассивных (не содержащих источников энергии) многополюсников. Покажем, что соединение резистивных элементов и лучевой звездой преобразуется в эквивалентную схему многоугольника с числом ветвей, равным n(n - 1)/2.
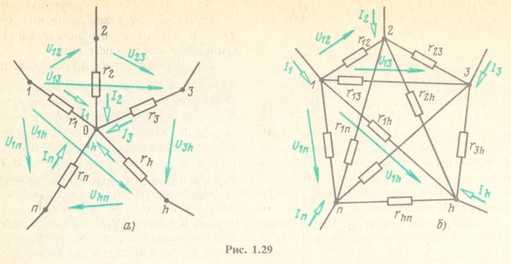
На рис. 1.29, а изображено соединение элементов в виде n-лучевой звезды. Для этой схемы
![]()
где ![]() - потенциалы соответствующих точек схемы.
- потенциалы соответствующих точек схемы.
Из последнего уравнения найдем потенциал точки О:
![]()
После подстановки ![]() в первое из выражений (1.73) получим
в первое из выражений (1.73) получим
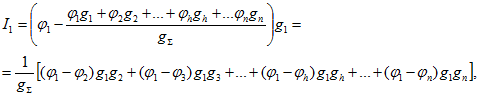
где
![]()
В полученном выражении разности потенциалов между точками 1, 2, 3,..,h,...,n заменим через напряжения по формуле ![]()
![]()
Аналогично для любого тока
![]()
Из этих уравнений видно, что ток каждой ветви n-лучевой звезды можно представить в виде суммы n - 1 частичных токов, пропорциональных напряжениям между соответствующими точками звезды. Например, ток ![]() Аналогично для любой ветви
Аналогично для любой ветви
![]()
Выражениям (1.76) удовлетворяет эквивалентная схема в виде полного многоугольника (рис. 1.29,6) с числом ветвей, равным n(n - 1)/2. Действительно, для схемы рис. 1.29,б
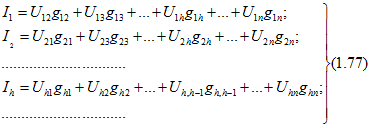
Для того чтобы схема, показанная на рис. 1.29,б была эквивалентна схеме на рис. 1.29, а, необходимо равенство токов (I1, I2, I3 и т. д.) в обеих схемах при одинаковых напряжениях (U12, U13, U1h и т. д.), что выполняется при
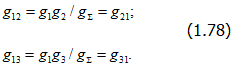
Поскольку число узлов многоугольника равно n число токов, связанных с каждым узлом, равно n - 1 и каждая ветвь присоединена к двум узлам многоугольника, то число его ветвей как раз равно n (n - 1)/2.
Из приведенного доказательства следует, что простая математическая операция исключения потенциала ![]() из системы уравнений для схемы, имеющей форму n-лучевой звезды, приводит к эквивалентной схеме в виде многоугольника. Обратная задача о преобразовании многоугольника в эквивалентную n-лучевую звезду в общем случае при n > 3 неразрешима, так как число искомых сопротивлений (или проводимостей) ветвей эквивалентной звезды меньше числа n (n - 1)/2 условий, которым они должны удовлетворять. При n = 3 число условий n (n - 1 )/2 = 3 и, следовательно, треугольник сопротивлений всегда можно преобразовать в эквивалентную звезду.
из системы уравнений для схемы, имеющей форму n-лучевой звезды, приводит к эквивалентной схеме в виде многоугольника. Обратная задача о преобразовании многоугольника в эквивалентную n-лучевую звезду в общем случае при n > 3 неразрешима, так как число искомых сопротивлений (или проводимостей) ветвей эквивалентной звезды меньше числа n (n - 1)/2 условий, которым они должны удовлетворять. При n = 3 число условий n (n - 1 )/2 = 3 и, следовательно, треугольник сопротивлений всегда можно преобразовать в эквивалентную звезду.
Из (1.78) при т = 3 сразу получаются формулы для преобразования трехлучевой звезды в эквивалентный треугольник в следующем виде:
для эквивалентных проводимостей
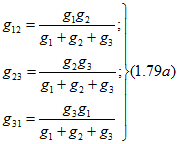
или для эквивалентных сопротивлений
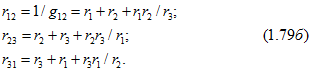
Чтобы получить формулы преобразования треугольника с заданными сопротивлениями r12, r23 и r31 в эквивалентную звезду, примем в (1.796) в качестве неизвестных сопротивления r1, r2 и r3. В результате получим
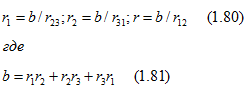
Выразим попарные произведения искомых сопротивлений в виде
![]()
и, подставив полученные выражения в (1.81), найдем
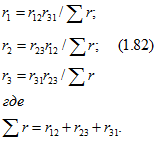
Последние формулы позволяют определить эквивалентные сопротивления звезды по заданным сопротивлениям треугольника.
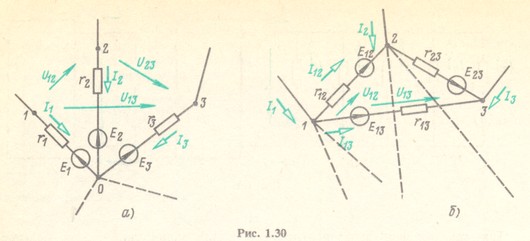
Аналогично можно получить формулы преобразования многолучевой звезды с источниками ЭДС (активной) (рис. 1.30, а) в эквивалентный активный многоугольник (рис. 1.30,6). Действительно, для схемы, показанной рис. 1.30, а, можно записать
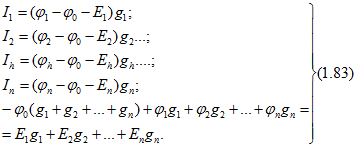
Выразив ![]() из последнего уравнения и подставив его, например, в первое из выражений (1.83), после элементарных преобразований получим
из последнего уравнения и подставив его, например, в первое из выражений (1.83), после элементарных преобразований получим
![]()
Аналогичные уравнения можно составить для токов I2, I3,...,In. Выражениям вида (1.84) соответствует эквивалентная схема, показанная на рис. 1.30,б. Проводимости ветвей многоугольника определяются попрежнему по (1.78), а эквивалентные ЭДС при указанных положительных направлениях (рис. 1.30, а и б)
![]()
Преобразование параллельного соединения ветвей с источниками ЭДС и источниками тока. Если сложная электрическая схема имеет одну или несколько групп параллельно соединенных ветвей с источниками ЭДС, то расчет и исследование такой схемы можно значительно упростить, заменив каждую группу параллельных ветвей одним источником с эквивалентной ЭДС и эквивалентным внутренним сопротивлением. В частности, так можно преобразовать схемы со смешанным соединением активных и пассивных элементов в схемы с последовательным соединением.
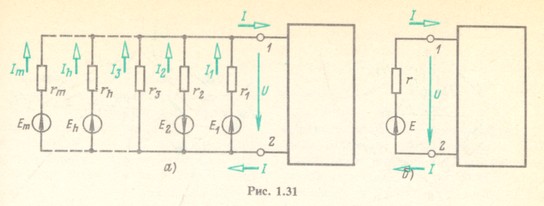
На рис. 1.31, a показана группа из m параллельно соединенных ветвей, выделенная из электрической схемы. Остальная часть схемы условно обозначена прямоугольником. Требуется заменить m параллельных ветвей (рис. 1.31, a) одной эквивалентной ветвью (рис. 1.31,6) так, чтобы на выводах 1 и 2 ток I и напряжение U в эквивалентной схеме, а значит, все токи и напряжения в остальной части схемы были такими же, как и в заданной. С учетом ( 1.11 б) для токов ветвей суммарный ток I схемы рис. 1.31, а
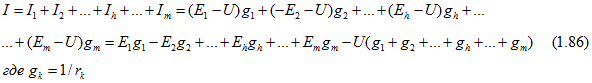
В схеме рис. 1.31,б ток
I=(E-U)g (1.87)
где g=1/r.
Так как условия эквивалентности должны быть выполнены при любых токе I и напряжении U, то, приравняв правые части выражений (1.86) и (1.87), нужно положить
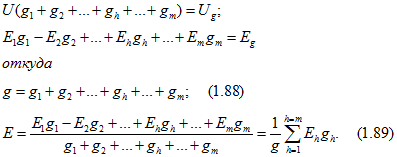
При вычислении эквивалентной ЭДС Е с положительным знаком записываются те ЭДС ![]() , которые направлены к тому же узлу, что и эквивалентная ЭДС Е, и с отрицательным знаком - направленные к другому узлу. Если какая-либо из параллельных ветвей, например третья, не содержит источника ЭДС Е3, то в (1.89) слагаемого
, которые направлены к тому же узлу, что и эквивалентная ЭДС Е, и с отрицательным знаком - направленные к другому узлу. Если какая-либо из параллельных ветвей, например третья, не содержит источника ЭДС Е3, то в (1.89) слагаемого ![]() не будет, но в состав проводимости g входит проводимость этой ветви g3.
не будет, но в состав проводимости g входит проводимость этой ветви g3.
Из (1.88) следует, что эквивалентная проводимость g не зависит от ЭДС, а эквивалентная ЭДС Е (1.89) зависит не только от ЭДС ветвей, но и от их проводимостей.
Выше было отмечено, что энергия, потребляемая сопротивлениями ветвей до преобразования схемы с активными элементами, не равна энергии, потребляемой эквивалентными сопротивлениями ветвей после преобразования.
Для иллюстрации этого положения сравним, например, мощности источников и потребителей заданной схемы (рис. 1.31, а) и схемы после преобразования (рис. 1.31,б) при разомкнутой ветви с током I. В схеме рис. 1.31, а при I = 0 токи I1и I2... могут и не быть равными нулю. В результате суммарная энергия источников ЭДС будет расходоваться на покрытие тепловых потерь в сопротивлениях ветвей. В схеме рис. 1.31,б при I = 0 потери в эквивалентном сопротивлении отсутствуют. Следовательно, несмотря на неизменность токов и напряжений в той части схемы, которая не затронута преобразованием, мощность, развиваемая источниками ЭДС до преобразования, не равна мощности, развиваемой эквивалентным источником ЭДС после преобразования схемы. Однако это обстоятельство не мешает широко пользоваться понятием эквивалентной ЭДС для расчета электрических цепей, так как после определения тока I и напряжения U в эквивалентной схеме можно вернуться к исходной и найти токи и мощности во всех ее ветвях.
Если к узлам 1 и 2 (рис. 1.31, я) присоединены кроме m ветвей с источниками ЭДС еще n ветвей с источниками тока, то при вычислении эквивалентной ЭДС (1.89) нужно учесть токи заданных источников тока:
![]()
причем с положительным знаком записываются токи, направленные к тому же узлу, что и эквивалентная ЭДС Е, а с отрицательным знаком - направленные к другому узлу.
Преобразование схемы с источниками ЭДС в эквивалентную схему с узловыми токами (источниками тока).
Выше было показано, что источник энергии с известным значением ЭДС и заданным внутренним сопротивлением можно представить источником тока, причем режим приемника энергии останется неизменным. Такую замену можно произвести и в том случае, если ветвь с источником ЭДС и внутренним сопротивлением имеет добавочное сопротивление, включенное последовательно с внутренним сопротивлением.
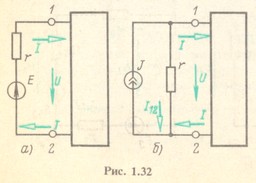
Пусть к выводам 1 и 2 (рис. 1.32, а) присоединена ветвь с источником ЭДС E и сопротивлением r, которое включает и внутреннее сопротивление источника энергии.
Обозначим напряжение между первым и вторым выводами U12 = U. По (1.11 б) ток
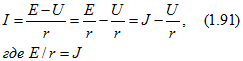
Из этого выражения следует, что ток I источника ЭДС может быть представлен в виде разности тока J источника тока, который определяется только параметрами ветви с источником ЭДС, и тока I12 = U/r. Уравнению (1.91) соответствует эквивалентная схема, показанная на рис. 1.32,6, в которой напряжение U и ток I те же, что и в схеме на рис. 1.32, а. Ток J источника тока направлен так же, как и ЭДС Е (от вывода 2 к выводу 1).
Такую замену можно провести в схеме как для одного, так и для всех или части источников ЭДС.
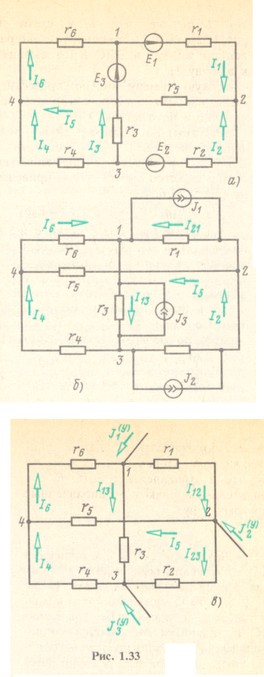
Рассмотрим, например, схему, показанную на рис. 1.33, а, с источниками ЭДС в трех ветвях. Эквивалентная схема с источниками тока приведена на рис. 1.33,б, где
![]()
На схеме рис. 1.33,б ветви с источниками тока J1, J2, J3 присоединены попарно к одним и тем же узлам 1, 2 и 3. Поэтому можно объединить в каждом узле два тока источников в один (рис. 1.33,в). Суммарные или узловые токи ![]() определяются по первому закону Кирхгофа:
определяются по первому закону Кирхгофа:
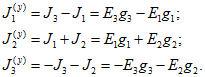
Следовательно, электрическая схема с источниками ЭДС в ветвях может быть заменена эквивалентной схемой с узловыми токами, причем потенциалы узлов и токи в непреобразоваиных ветвях остаются неизменными. Так, токи I4, I5 и I6 заданной схемы (рис. 1.33, а) равны токам в тех же ветвях эквивалентной схемы (рис. 1.33,б или в), но, конечно, токи в преобразуемых ветвях с источниками ЭДС не равны соответствующим токам в ветвях эквивалентной схемы. Например, в сопротивлении r1 заданной схемы (рис. 1.33, а) ток ![]() , a в эквивалентной схеме (рис. 1.33,в) ток
, a в эквивалентной схеме (рис. 1.33,в) ток ![]() .
.
В общем случае справедливость преобразования схемы с источниками ЭДС в ветвях в эквивалентную схему с узловыми токами непосредственно следует из уравнений узловых потенциалов. Действительно, для схемы рис. 1.33, а на основании уравнений (1.33) при ![]() получим
получим
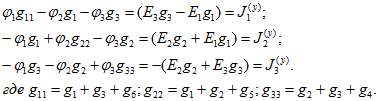
Этим уравнениям удовлетворяет эквивалентная схема (рис. 1.33, в).
Обратная замена электрической схемы с заданными узловыми токами эквивалентной схемой с источниками ЭДС не является однозначной. Это объясняется тем, что число узловых токов или число узлов всегда меньше числа ветвей, т. е. количество уравнений, которое можно составить на основании первого закона Кирхгофа, меньше числа искомы ЭДС. Поэтому можно задаться произвольными значениями ЭДС источников в любых ветвях в количестве, равном числу недостающих уравнений. Остальные неизвестные ЭДС могут быть определены после совместного решения независимых уравнений, составленных по первому закону Кирхгофа.
Пример 1.5.
Определить токи во всех ветвях и составить уравнения баланса мощ-ностей для схемы рис. 1.34, а, если Е1 =48 В, Е2 = 24 В, Е3 = 12 В, Е = 12 В, r1 = 3 Ом, r2 = 6 Ом, r3 = r4 = 2 Ом, r = 6 Ом.
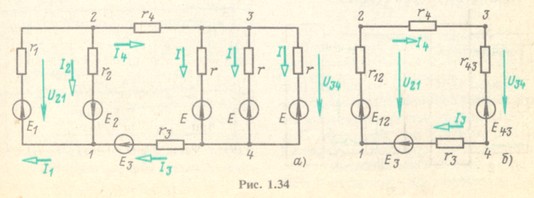
Решение.
Для определения токов I4 и I3 (эти токи одинаковы) заменим каждую группу параллельно соединенных ветвей од-ной эквивалентной. Эквивалентную ЭДС Е12 для первой и второй параллельных ветвей и эквивалентное сопротивление r12 определим по (1.89) и (1.88):
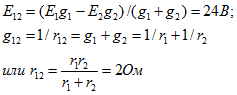
Аналогично находим эквивалентное сопротивление и эквивалентную ЭДС для трех параллельных ветвей, присоединенных к третьему и четвертому узлам:
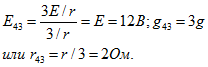
В результате таких преобразований получается схема, показанная на рис. 1.34,б. В этой схеме ток
![]()
и напряжения на участках
![]()
Токи в ветвях заданной схемы
![]()
Токи в ветвях с одинаковыми ЭДС Е равны друг другу и направлены навстречу ЭДС:
![]()
Суммарная мощность всех источников ЭДС
![]()
Мощность в сопротивлениях, конечно, равна суммарной мощности источников ЭДС:
![]()
Отметим, что источники ЭДС Е работают в режиме приемников, потребляя энергию от других источников.
Смотри ещё по теме Электрические цепи постоянного тока
Основные законы и методы расчета электрических цепей постоянного тока
- Элементы электрических цепей и схем
- Схемы замещения источников энергии
- Закон Ома для участка цепи с ЭДС
- Баланс мощностей для простой неразветвленной цепи
- Законы Кирхгофа и их применение
- Топологические графы
- Законы Кирхгофа в матричной форме
- Метод узловых потенциалов
- Метод контурных токов
- Уравнения цепи в матричной форме
- Расширенные узловые уравнения
- Преобразования в линейных электрических схемах
Основные свойства электрических цепей постоянного тока
- Принцип наложения (суперпозиции)
- Свойство взаимности
- Входные и взаимные проводимости, коэффициенты передачи
- Принцип компенсации. Зависимые источники
- Общие замечания о двухполюсниках и многополюсниках
- Линейные соотношения между напряжениями и токами
- Теорема о взаимных приращениях токов и напряжений
- Принцип эквивалентного генератора
- Передача энергии от активного двухполюсника к пассивному

