Включение rL-цепи на постоянное напряжение

Дифференциальное уравнение при включении rL-цепи (рис. 14.5) на постоянное напряжение (к источнику ЭДС E = U) неоднородное

и имеет решение в виде суммы установившейся и свободной составляющих

Установившаяся составляющая тока .

Однородное уравнение совпадает с ( 14.4), и его решение - с ( 14.8). Ток в цепи

где t=L/r.

Постоянная интегрирования А определяется с учетом известного начального условия. До коммутации тока в цепи не было, поэтому согласно первому закону коммутации при t=0

Напряжение на индуктивности

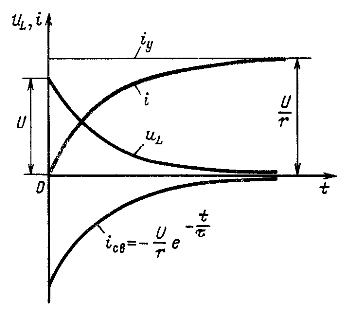
Поскольку до включения напряжение на индуктивном элементе было равно нулю, а момент коммутации , то переходное и свободное напряжения на индуктивности изменяются скачком. Кривые изменения приведены на рис. 14.6. Как и следовало ожидать, они показывают, что ток в цепи не устанавливается мгновенно и что требуется известное время (теоретически бесконечное) до наступления установившегося режима со значением тока U/r. Ток i возрастает тем медленнее, чем больше постоянная времени цепи t, т. е. чем медленнее затухает свободный ток.

Энергия, получаемая от источника, идет частично на увеличение энергии магнитного поля катушки, а частично переходит в тепло.

Рис. 14.5

Рис. 14.6

Пример 14.1.

В цепи с параметрами , подключенной к источнику постоянной ЭДС с напряжением U = 220 В (рис. 14.7), происходит внезапное уменьшение сопротивления от значения до (ключ замыкает некоторую часть резистора с сопротивлением ). Найти закон изменения тока в цепи.

Решение. На основании (14.8) и (14.5) напишем сразу выражение для свободного тока

и для переходного тока

Из условия отсутствия скачка тока i при t = 0 получаем

откуда А = -7,3.

Следовательно, .

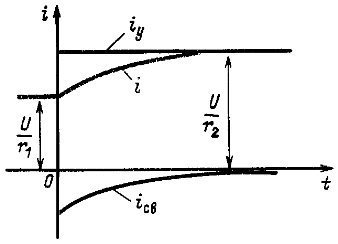
Отметим, что постоянная времени цепи после коммутации определяется параметрами . Кривые токов показаны на рис. 14.8. Из них видно, что ток i постепенно возрастает от меньшего значения до большего .

Переходный процесс при внезапном увеличении сопротивления аналогичен рассмотренному, только ток будет постепенно уменьшаться.

Рис. 14.7

Рис. 14.8

Дополнительно по теме