Запись интеграла Дюамеля при помощи импульсной переходной характеристики

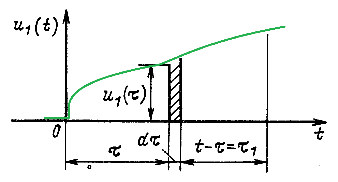
Пусть на входе пассивной системы или цепи действует источник непрерывно изменяющегося напряжения (или тока) (рис. 14.40). Определим реакцию на выходе, например ток в момент времени t.

Разобьем кривую на отдельные импульсы шириной dt и высотой для момента времени t=t. Для единичного импульса, действующего в момент времени t, реакция на выходе по определению равна импульсной переходной характеристике k(t - t), где t -t - промежуток времени от момента t действия импульса до момента t. Но площадь рассматриваемого импульса не равна единице, а равна . Поэтому реакция от него на выходе в момент t будет равна . Суммируя действия всех импульсов, каждый из которых имеет бесконечно малую площадь, от t=0 до t=t, получаем реакцию на выходе

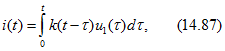
или с учетом (14.79)

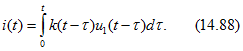
При напряжении произвольной формы (см. рис. 14.34) по формулам (14.87) или (14.88) определяется ток в интервале времени . В промежутке

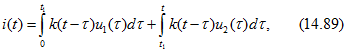
или

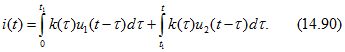
Рис. 14.40

При нужно, очевидно, заменить верхний предел t у второго интеграла на .

Реакции цепи h(t) и k(t) на действие единичного скачка и единичного импульса, а значит, и применения интегралов Дюамеля предполагают нулевые начальные условия. В противном случае необходимо воспользоваться методом наложения.

Если переходная или импульсная переходная характеристика известна (найдена), то интегралы Дюамеля можно найти при помощи стандартных программ.

Дополнительно по теме