Переходная и импульсная переходная характеристики

В линейной теории цепей автоматического управления и в других дисциплинах часто пользуются понятиями переходной характеристики и импульсной переходной характеристики какой-либо системы или цепи.

Аналогично вводят понятие переходной характеристики любой цепи или системы, например для четырехполюсника переходной характеристикой называется реакция (напряжение или ток) на выходе при единичном ступенчатом воздействии на входе.

Понятие переходной характеристики h(t) как реакции (отклика) системы (или как выходной величины, за которую может быть принята любая из функций системы) на единичное ступенчатое воздействие, приложенное к ее входу (причем, за вход системы может быть принята любая ветвь или два вывода), применимо не только к электрическим цепям, но и к любым физическим системам - механическим, пневматическим, гидравлическим, электромеханическим и т. д. Так, переходные характеристики rL-, rС- и rLC-цепей, если, например, в качестве выходной величины выбраны токи, даются формулами ( 14.14), ( 14.26), ( 14.60), ( 14.63) при U = 1, а если выбраны напряжения на емкостных элементах, то формулами ( 14.25), ( 14.59), ( 14.62) также при U = 1.

Переходная характеристика введена в основном по двум причинам.

1. Единичное ступенчатое воздействие 1(t) - скачкообразное, и поэтому довольно тяжелое для любой системы внешнее воздействие. Следовательно, важно знать реакцию системы именно при таком воздействии. Иные, например, всевозможные плавные воздействия будут для системы легче.

2. Если определена характеристика h(t), то при помощи интеграла Дюамеля (см. раздел и раздел) можно определить реакцию системы при любой форме внешних воздействий.

Существует еще один вид внешнего воздействия, называемый единичным импульсом, дельта-функцией d(t) или функцией Дирака, которое определяется как производная

по времени единичной функции

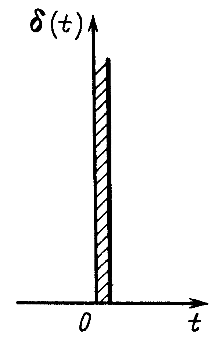
и представляет собой предельный случай импульса очень большого значения и очень малой продолжительности (рис. 14.39), когда его длительность стремится к нулю, но площадь сохраняется равной единице.

Действительно, оставляя сейчас в стороне вопрос о законности операций дифференцирования разрывной функции 1(t), но отметив, что в теории обобщенных функций эти операции достаточно строго обоснованы, найдем площадь единичного импульса:

Рис. 14.39

Импульсной переходной функцией или характеристикой (весовой функцией) системы (например, четырехполюсника) k(t) называется реакция на выходе, если на входе действует внешнее возмущение в виде единичного импульса d(t). Поскольку внешние возмущения 1(t) и d(t) связаны равенством (14.83), то при h(0+)=0 получаем, что подобным же равенством связаны и их реакции на выходе системы, т. е.

В справедливости (14.84) можно убедиться непосредственно, вычислив h(t), k(t) и dh(t)/dt для любой цепи.

Если же , то соотношение (14.84) обобщается:

Например, если при включении rС-цепи на единичный импульс напряжения в качестве выходной величины рассматривается ток, то

Так как при t - 0 в составе приложенного напряжения имеется дельта-функция и в этот момент по второму закону коммутации , то дельта-функция должна быть и в составе тока, что и объясняет наличие второго слагаемого в правой части (14.85).

Импульсная переходная характеристика k(t) введена по тем же двум причинам, что и h(t).

1. Единичный импульс - скачкообразное и поэтому довольно тяжелое возмущение для системы или цепи; оно тяжелее, чем плавное возмущение. Следовательно, важно знать реакцию системы или цепи на это возмущение.

2. При помощи некоторого видоизменения интеграла Дюамеля можно, зная k(t), вычислить реакцию системы или цепи на любое внешнее возмущение (см. раздел).

Реализацию внешнего воздействия в виде единичного импульса напряжения d(t) обычно представляют как экспоненциальное воздействие с очень большой начальной ординатой и очень малой постоянной времени t, так что

где - площадь, ограничиваемая экспоненциальным импульсом, т. е.

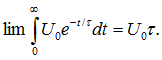
Дополнительно по теме