Включение пассивного двухполюсника к источнику напряжения произвольной формы
В дальнейшем под произвольной формой напряжения будем понимать его изменение, определяемое кусочно-аналитической функцией, т. е. функцией, аналитически заданной на каждом конечном интервале и имеющей в точках стыка интервалов разрывы непрерывности первого рода.
Пусть произвольный пассивный двухполюсник подключается к источнику напряжения, кривая изменения которого дана на рис. 14.34. Для вычисления тока определим, как и выше, переходную функцию h(t).
Так как в промежутке ![]() включаемое напряжение задано функцией
включаемое напряжение задано функцией ![]() , то, воспользовавшись формулой ( 14.78), можем написать для этого промежутка времени
, то, воспользовавшись формулой ( 14.78), можем написать для этого промежутка времени
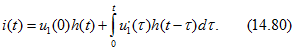
В следующем промежутке ![]() напряжение задано другой функцией
напряжение задано другой функцией ![]() , причем в момент
, причем в момент ![]() оно изменяется скачком от значения
оно изменяется скачком от значения ![]() до значения
до значения ![]() . Для учета скачка напряжения в точке
. Для учета скачка напряжения в точке ![]() будем считать, что в этот момент к двухполюснику прикладывается отрицательное постоянное напряжение, равное
будем считать, что в этот момент к двухполюснику прикладывается отрицательное постоянное напряжение, равное ![]() . Кроме того, учтем составляющие тока от начального скачка напряжения
. Кроме того, учтем составляющие тока от начального скачка напряжения ![]() и от элементарных скачков напряжения, определяемого кривой
и от элементарных скачков напряжения, определяемого кривой ![]() и действующего от t = 0 до
и действующего от t = 0 до ![]() .
.
В результате получим
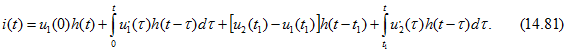
В этом равенстве в третьем члене аргументом переходной функции служит величина ![]() так как напряжение
так как напряжение ![]() включается в момент
включается в момент ![]() . Аргумент t - t переходной функции в обоих интегралах один и тот же, поскольку он имеет смысл промежутка времени, прошедшего от включения элементарного скачка напряжения Du до рассматриваемого момента времени t (см. рис. 14.32, а). Однако, разумеется, пределы изменения t в обоих интегралах различны.
. Аргумент t - t переходной функции в обоих интегралах один и тот же, поскольку он имеет смысл промежутка времени, прошедшего от включения элементарного скачка напряжения Du до рассматриваемого момента времени t (см. рис. 14.32, а). Однако, разумеется, пределы изменения t в обоих интегралах различны.
Наконец, для промежутка времени ![]() учтем, что в момент
учтем, что в момент ![]() включается постоянное напряжение
включается постоянное напряжение ![]() и что элементарные скачки, определяемые кривой напряжения
и что элементарные скачки, определяемые кривой напряжения ![]() , действуют до момента времени
, действуют до момента времени ![]() . Поэтому
. Поэтому
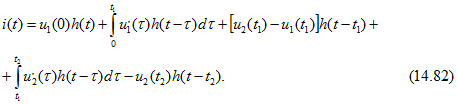
Рассмотрим еще переходные процессы при включении произвольного активного двухполюсника к источнику напряжения любой формы.
Найдем ток i в любой ветви активного двухполюсника (в частности, и в ветви ключа). Расчет проведем по принципу наложения. Сначала будем считать двухполюсник пассивным, т. е. учтем только включаемый источник напряжения u(t). Расчет тока при этом проведем по формулам Дюамеля. Затем учтем только источники активного двухполюсника, т. е. найдем ток в той же ветви, считая, что источник напряжения не действует и что его внутреннее сопротивление равно нулю. Расчет тока в этом случае выполним, например, классическим методом (см. раздел). Суммируя найденные составляющие токи, получаем искомый ток.
Отметим еще, что при подаче на вход активного двухполюсника ряда импульсов напряжения (рис. 14.35) расчет токов в любой ветви также можно провести при помощи формулы Дюамеля.
При действии последовательности прямоугольных импульсов расчет можно вести и без применения формулы Дюамеля. В самом деле, для учета действия любого прямоугольного импульса можно считать, что в момент начала его действия включается источник постоянного напряжения, равный численно напряжению импульса, а в момент окончания действия импульса включается такой же источник с напряжением противоположного знака.
Рис. 14.34
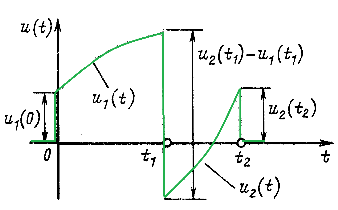
Рис. 14.35
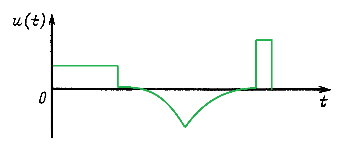
Рис. 14.37
Пример 14.5.
Найти ток ![]() (рис. 14.36) для промежутков времени
(рис. 14.36) для промежутков времени ![]() , если
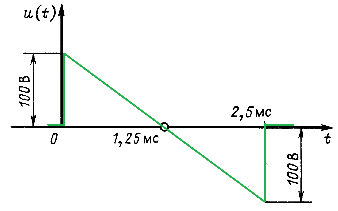
, если ![]() при u(t), показанном на рис. 14.37.
при u(t), показанном на рис. 14.37.
Решение. Переходная функция тока
![]()
где ![]() (цепь с одним индуктивным элементом) и по ( 14.18) постоянная времени
(цепь с одним индуктивным элементом) и по ( 14.18) постоянная времени
![]()
При t = 0 по первому закону коммутации ![]() , т. е. и h(0) = 0, следовательно, А = -0,5 и
, т. е. и h(0) = 0, следовательно, А = -0,5 и ![]() .
.
Уравнение напряжения источника (рис. 14.37)
u(t)= 100(1 - 800t) В.
Применяя формулу Дюамеля (14.80) для промежутка ![]() , получаем
, получаем
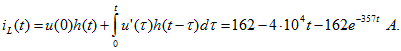
Проверив, убедимся, что ![]() .
.
Для промежутка времени ![]() согласно (14.81)
согласно (14.81)
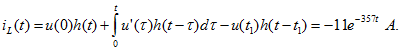
При ![]() ток
ток ![]() измениться не должен, несмотря на скачок напряжения источника. Проверив, убедимся, что
измениться не должен, несмотря на скачок напряжения источника. Проверив, убедимся, что
![]()
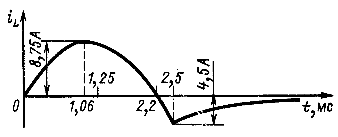
Кривая тока ![]() приведена на рис. 14.38.
приведена на рис. 14.38.
Рис. 14.38
Дополнительно по теме
- Переходные процессы в электрических цепях
- Возникновение переходных процессов и законы коммутации
- Переходный, установившийся и свободный процессы
- Короткое замыкание rL-цепи
- Включение rL-цепи на синусоидальное напряжение
- Короткое замыкание rС-цепи
- Включение rC-цепи на постоянное напряжение
- Включение rC-цепи на синусоидальное напряжение
- Переходные процессы в rС-цепи
- Апериодическая разрядка конденсатора
- Предельный случай апериодической разрядки конденсатора
- Периодическая (колебательная) разрядка конденсатора
- Включение rLC-цепи на постоянное напряжение
- Общий случай расчета переходных процессов классическим методом
- Пример классического метода
- Переходные процессы в цепях с взаимной индуктивностью
- Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
- Переходная и импульсная переходная характеристики
- Запись интеграла Дюамеля при помощи импульсной переходной характеристики
- Метод переменных состояния
- Численные методы решения уравнений состояния
- Дискретные модели электрической цепи
- Переходные процессы при некорректных коммутациях
- Определение переходного процесса при воздействии периодических импульсов напряжения

