Метод переменных состояния
Уравнениями состояния можно назвать любую систему уравнений, определяющих режим цепи. В более узком смысле - это система дифференциальных уравнений первого порядка, разрешенная относительно производных.
Методом переменных состояния назовем анализ цепи, основанный на решении уравнений состояния (первого порядка), записанных в форме Коши. Таким образом, метод переменных состояния - один из методов расчета прежде всего переходных процессов. Далее предполагается, что цепь имеет только независимые источники и не содержит индуктивных сечений и емкостных контуров. В противном случае составление уравнений становится намного сложнее.
Для линейной цепи с постоянными сосредоточенными параметрами ток каждой ветви, напряжение между выбранными выводами, заряд на обкладках конденсатора и т. д. всегда можно найти как решение составленного для этого тока, напряжения, заряда и т. д. дифференциального уравнения (например, исключением других токов и напряжений из системы уравнений Кирхгофа):
![]()
Введением переменных ![]() это уравнение сводится к эквивалентной системе дифференциальных уравнений первого порядка:
это уравнение сводится к эквивалентной системе дифференциальных уравнений первого порядка:
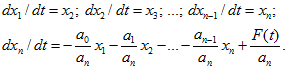
Здесь переменными, которые называются переменными состояния, служат переменная х и ее производные.
Как известно, переходный процесс в любой цепи, кроме ее параметров (значений r, L, С, М) и действующих источников [e(t) и J(t)], определяется независимыми начальными (t = 0) условиями - токами в индуктивных элементах ![]() и напряжениями на емкостных элементах
и напряжениями на емкостных элементах ![]() , которые должны быть известны или рассчитаны. Через них выражаются искомые величины во время переходного процесса. Они же определяют энергетическое состояние цепи. Поэтому в качестве переменных состояния целесообразно выбирать токи
, которые должны быть известны или рассчитаны. Через них выражаются искомые величины во время переходного процесса. Они же определяют энергетическое состояние цепи. Поэтому в качестве переменных состояния целесообразно выбирать токи ![]() и напряжения
и напряжения ![]() . Действующие источники можно назвать входными величинами
. Действующие источники можно назвать входными величинами ![]() , искомые величины - выходными
, искомые величины - выходными ![]() . Для цепи с n независимыми токами
. Для цепи с n независимыми токами ![]() и напряжениями
и напряжениями ![]() должны быть заданы еще n независимых начальных условий.
должны быть заданы еще n независимых начальных условий.
Сокращенно дифференциальные уравнения состояния запишем в матричной форме так:
![]()
или короче
![]()
где X матрица-столбец (размера n x 1) переменных состояния (вектор переменных состояния); F - матрица-столбец (размера m x 1) ЭДС и токов источников (внешних возмущений); А - квадратная матрица порядка n (основная); В - матрица размера п х m (матрица связи). Элементы этих матриц определяются топологией и параметрами цепи.
Для выходных величин (если определяются не токи в индуктивных и напряжения на емкостных элементах) в матричной форме система алгебраических уравнений имеет вид
![]()
или короче
![]()
где W - матрица-столбец (размера l x 1); M - матрица связи (размера l x n); N - матрица связи (размера l x m).
Элементы матриц зависят от топологии и параметров цепи. Для уравнений состояния разработаны и машинные алгоритмы формирования на основе топологии и значений параметров.
Уравнения в матричной форме (14.91) можно составить, например, с применением метода наложения. Для получения зависимостей между производными переменных состояния, т. е. ![]() и переменными состояния
и переменными состояния ![]() , а также ЭДС и токами источников, действующими в цепи, будем считать, что переменные состояния заданы. Рассматриваемую цепь, например на рис. 14.41, а, заменим после коммутации эквивалентной (рис. 14.41,6), у которой каждый заданный ток
, а также ЭДС и токами источников, действующими в цепи, будем считать, что переменные состояния заданы. Рассматриваемую цепь, например на рис. 14.41, а, заменим после коммутации эквивалентной (рис. 14.41,6), у которой каждый заданный ток ![]() представлен источником тока
представлен источником тока ![]() , а каждое заданное напряжение
, а каждое заданное напряжение ![]() - источником напряжения (ЭДС)
- источником напряжения (ЭДС) ![]() . Применив метод наложения (положительные направления выбраны), запишем напряжения
. Применив метод наложения (положительные направления выбраны), запишем напряжения ![]() и токи
и токи ![]() (сначала учитываем действие источников
(сначала учитываем действие источников ![]() затем
затем ![]() и далее источников, действующих в цепи):
и далее источников, действующих в цепи):
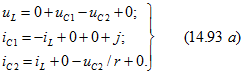
Рис. 14.41
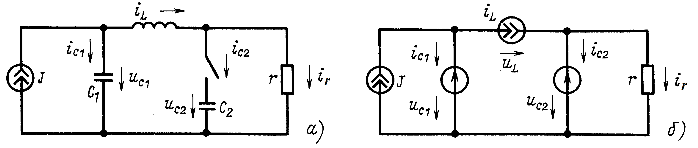
Так как ![]() , то
, то
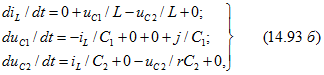
т. e.
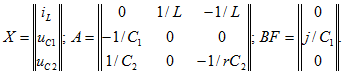
Конечно, уравнения (14.93) можно получить и из уравнений Кирхгофа исключением токов и напряжений ре-зистивных элементов. Однако совместное решение уравнений Кирхгофа с увеличением числа ветвей цепи становится все более громоздким.
Уравнения состояния можно формировать и сразу в матричной форме.
Если источников тока и ЭДС нет, т. е. F = 0, то уравнения (14.91) упрощаются
![]()
и характеризуют свободные процессы в цепи. Решение запишем в виде
![]()
где X (0) - матрица-столбец начальных значений переменных состояния; ![]() - матричная экспоненциальная функция.
- матричная экспоненциальная функция.
Подставив (14.94) в (14.91в), убедимся, что получается тождество.
При ![]() решение уравнения (14.91) представим в виде
решение уравнения (14.91) представим в виде
![]()
где Ф(t) - некоторая матричная функция цепи. После дифференцирования (14.95) получим
![]()
Сравним (14.96) с (14.91а)
![]()
и, умножив на ![]() , после интегрирования найдем, что
, после интегрирования найдем, что
![]()
где q - переменная интегрирования, или
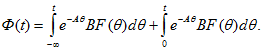
Подставим это выражение в (14.95):

В частности, при t = 0 имеем ![]()
Следовательно, решение для переменных состояния записывается в виде
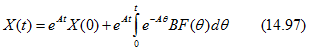
(реакция цепи равна сумме реакций при нулевом входе и при нулевом начальном состоянии).
Это решение можно получить и применив операторный метод расчета переходных процессов, рассматриваемый в разделе.
Выходные величины можно найти по (14.92).
Если состояние цепи задано не при t = 0, а при ![]() , то в (14.97) первое слагаемое записывается так:
, то в (14.97) первое слагаемое записывается так: ![]() , а нижний предел интеграла не 0, а t.
, а нижний предел интеграла не 0, а t.
Главная трудность расчета заключается в вычислении матричной экспоненциальной функции. Один из путей такой: сначала находим собственные значения l матрицы А, т. е. корни уравнения
![]()
где 1 - единичная матрица порядка n, которые определяются из уравнения
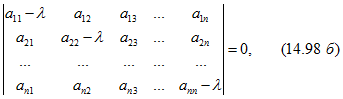
где ![]() - элементы матрицы А.
- элементы матрицы А.
Собственные значения совпадают с корнями ![]() характеристического уравнения цепи.
характеристического уравнения цепи.
Матричная экспонента, аргумент которой - матрица Аt, имеющая порядок n, представима конечным числом n слагаемых. Если собственные значения различны, то
![]()
где ![]() - функции времени;
- функции времени; ![]() и т. д.
и т. д.
Далее для определения ![]() составляем алгебраическую систему n уравнений
составляем алгебраическую систему n уравнений
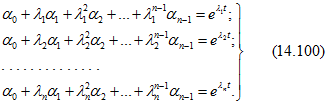
Наконец, определив ![]() из (14.100), по (14.99) находим
из (14.100), по (14.99) находим ![]() и затем X (t) по (14.97).
и затем X (t) по (14.97).
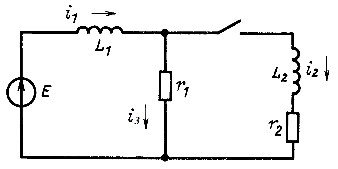
Пример 14.6. Определить ток ![]() в цепи на рис. 14.42 после коммутации при
в цепи на рис. 14.42 после коммутации при ![]() .
.
Решение. Выбираем положительные направления токов ![]() в индуктивных элементах, т. е. переменных состояния, и тока
в индуктивных элементах, т. е. переменных состояния, и тока ![]() . Независимые начальные условия:
. Независимые начальные условия: ![]() . Дифференциальные уравнения цепи
. Дифференциальные уравнения цепи
![]()
Рис. 14.42
Исключив ток ![]() , получим уравнения относительно производных переменных состояния:
, получим уравнения относительно производных переменных состояния:
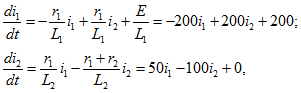
т. е. согласно (14.91)
![]()
и матрица-столбец начальных значений
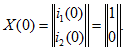
Вычислим собственные значения; по (14.98)
![]()
откуда ![]() . Если приравнять нулю главный определитель уравнений с переменными состояния, то получим те же значения
. Если приравнять нулю главный определитель уравнений с переменными состояния, то получим те же значения ![]() .
.
Находим коэффициенты ак по (14.100), т. е. из системы уравнений
![]()
откуда
![]()
и по (14.99)
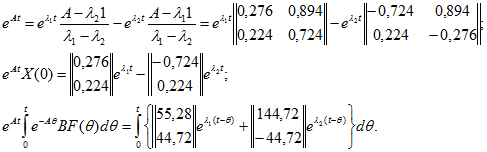
Ток
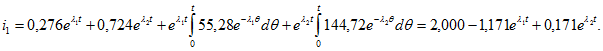
Значения тока ![]() вычисленные в моменты
вычисленные в моменты ![]() секунд для интервала времени 0 - 0,1 с, в конце которого ток отличается от установившегося
секунд для интервала времени 0 - 0,1 с, в конце которого ток отличается от установившегося ![]() менее чем на 1,5%, приведены в табл. 14.1. При вычислениях цифры записывались с 8 разрядами, а во всех приведенных в примере формулах и в табл. 14.1 указаны с округлением.
менее чем на 1,5%, приведены в табл. 14.1. При вычислениях цифры записывались с 8 разрядами, а во всех приведенных в примере формулах и в табл. 14.1 указаны с округлением.
Таблица 14.1
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0,005 |
0,010 |
0,015 |
0,020 |
0,025 |
0,030 |
0,035 |
0,040 |
0,045 |
0,050 |
|
1,079 |
1,213 |
1,343 |
1,455 |
1,550 |
1,628 |
1,692 |
1,746 |
1,790 |
1,827 |
k |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
0,055 |
0,060 |
0,065 |
0,070 |
0,075 |
0,080 |
0,085 |
0,090 |
0,095 |
0,100 |
|
1,857 |
1,882 |
1,902 |
1,919 |
1,933 |
1,945 |
1,954 |
1,962 |
1,970 |
1,974 |
Если среди n собственных значений матрицы А есть q кратных ![]() , то для n - q разных корней составляется система (14.100), а для q кратных уравнения получаются после вычисления первых q - 1 производных по
, то для n - q разных корней составляется система (14.100), а для q кратных уравнения получаются после вычисления первых q - 1 производных по ![]() от обеих частей уравнения с корнем
от обеих частей уравнения с корнем ![]() , т. е.
, т. е.
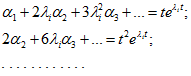
Если в цепи действует только один источник ЭДС (или тока), представляющий единичный скачок 1(t), т. е. F(t)=1(t), и начальные условия нулевые, то решение (14.97) запишется в виде
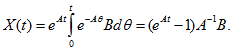
Для выходных величин по (14.92а) получим
![]()
Это будут переходные функции цепи h(t). Импульсные переходные функции k(t) определяются по (14.84) или (14.85).
Более общим путем вычисления матричной экспоненциальной функции служит ее представление бесконечным рядом
![]()
но ряд при больших t медленно сходится. При ограничении конечным числом слагаемых вычисление сводится к умножению и суммированию матриц. Такие операции есть в математическом обеспечении ЭВМ. Известен метод вычисления матричной экспоненциальной функции, основанный на критерии Сильверста.
Уравнения состояния цепей, порядок которых больше двух-трех, проще решаются не аналитическими, а численными методами, дающими возможность автоматизировать расчет в случае применения ЭВМ.
Дополнительно по теме
- Переходные процессы в электрических цепях
- Возникновение переходных процессов и законы коммутации
- Переходный, установившийся и свободный процессы
- Короткое замыкание rL-цепи
- Включение rL-цепи на синусоидальное напряжение
- Короткое замыкание rС-цепи
- Включение rC-цепи на постоянное напряжение
- Включение rC-цепи на синусоидальное напряжение
- Переходные процессы в rС-цепи
- Апериодическая разрядка конденсатора
- Предельный случай апериодической разрядки конденсатора
- Периодическая (колебательная) разрядка конденсатора
- Включение rLC-цепи на постоянное напряжение
- Общий случай расчета переходных процессов классическим методом
- Пример классического метода
- Переходные процессы в цепях с взаимной индуктивностью
- Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
- Включение пассивного двухполюсника к источнику напряжения произвольной формы
- Переходная и импульсная переходная характеристики
- Запись интеграла Дюамеля при помощи импульсной переходной характеристики
- Численные методы решения уравнений состояния
- Дискретные модели электрической цепи
- Переходные процессы при некорректных коммутациях
- Определение переходного процесса при воздействии периодических импульсов напряжения

