Короткое замыкание rС-цепи

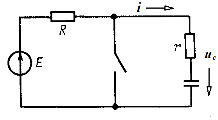
Предположим, что конденсатор емкостью С был заряжен от источника постоянной ЭДС (рис. 14.11) до напряжения , а затем замкнулся ключ и конденсатор разряжается через резистор r.

Ветвь с резистором и конденсатором в дальнейшем будем называть сокращенно rС-цепью.

Исследуем возникающий переходный процесс.

Установившееся напряжение на конденсаторе и установившийся ток i равны нулю. Ток и напряжение равны свободным составляющим.

Выберем положительные направления напряжения на конденсаторе и тока совпадающими (как и при расчете режимов в цепях переменного тока), так что ток

Запишем уравнение второго закона Кирхгофа для цепи после коммутации

На основании (14.19) и (14.20а) составим дифференциальное уравнение для напряжения:

Это однородное уравнение первого порядка. Соответствующее характерис-тическое уравнение

имеет корень Общее решение

Рис. 14.11

Величина t=rС, имеющая размерность времени, называется постоянной времени rC-пепи. Обратная ей величина a = 1/t = 1/rС называется коэффициентом затухания rC-цени. Постоянная времени t тем больше, чем больше емкость и сопротивление. Следовательно, чем больше емкость С и сопротивление r, тем медленнее в цепи затухают свободные ток и напряжение, тем медленнее происходит разрядка конденсатора.

Постоянную интегрирования А определим из начальных условий. Согласно закону коммутации напряжение на емкости в момент коммутации (т. е. при t = 0) не может измениться скачком, поэтому

Для напряжения на конденсаторе получим:

и ток согласно (14.19)

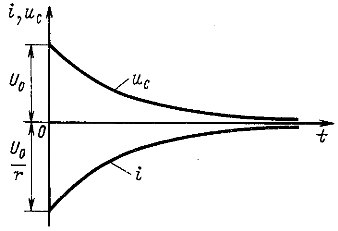
Кривые изменения и i приведены на рис. 14.12.

С энергетической точки зрения процесс короткого замыкания rC-цепи характеризуется переходом энергии, запасенной до коммутации в электрическом поле конденсатора, в тепло в резисторе

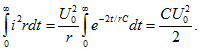
Отметим, что практически ветвь с сопротивлением и емкостью всегда имеет и какую-то индуктивность, хотя бы и очень малую. Поэтому и в данном случае ток начнется с нуля (т. е. не изменится скачком), но очень быстро достигнет значения, весьма близкого к , и затем будет уменьшаться практически экспоненциально (14.23).

Если конденсатор в цепи рис. 14.11 до включения рубильника питался от источника синусоидальной ЭДС, то - значение напряжения на конденсаторе в момент коммутации.

Если положительное направление тока i (рис. 14.11) выбрать противоположным положительному направлению напряжения , то знаки в формулах (14.19) и (14.23) изменятся на обратные.

Рис. 14.12

Дополнительно по теме