Переходные процессы в rLC-цепи (последовательном контуре)

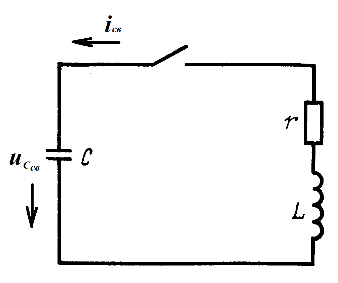
По второму закону Кирхгофа свободные напряжения на всех элементах неразветвленной цепи взаимно уравновешиваются. Поэтому в последовательном контуре при отсутствии источников, т. е. при (рис. 14.16),

где

Подставляя значение i в уравнение (14.30), после дифференцирования получаем для дифференциальное уравнение второго порядка:

Заряд на конденсаторе удовлетворяет такому же дифференциальному уравнению :

Дифференцируя это уравнение по времени, с учетом (14.31) получаем аналогичное дифференциальное уравнение для i:

Тождественность дифференциальных уравнений указывает на одинаковый закон изменения .

Для решения любого из этих дифференциальных уравнений составим характеристическое уравнение

Характер свободного процесса зависит только от параметров rLC-цепи, т. е., иначе говоря, от вида корней характеристического уравнения. Так как эти корни определяются равенством

то характер свободного процесса зависит от знака подкоренного выражения, который и определяет, будут ли корни действительными или комплексными.

Рис. 14.16

Дополнительно по теме