Операторный метод расчета переходных процессов. Применение преобразования Лапласа к расчету переходных процессов

Классический метод расчета переходных процессов требует в общем случае многократного решения систем алгебраических уравнений для нахождения начальных значений функции и ее производных, что и представляет основную трудность расчета этим методом, и для определения постоянных интегрирования по начальным условиям.

Так как дифференциальные уравнения переходных процессов в линейных цепях с сосредоточенными параметрами представляют собой линейные уравнения с постоянными коэффициентами, то их можно интегрировать также операторным методом, основанным на преобразовании Лапласа. Это было впервые показано русским математиком М.Е.Ващенко-Захарченко в его монографии "Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений" (Киев, 1862). В конце XIX в. английский ученый О. Хевисайд независимо пришел к операторному методу и впервые применил его к расчету электромагнитных переходных процессов. Однако Хевисайд не приводил математических обоснований метода. Дальнейшему развитию операторного исчисления способствовали своими трудами советские и зарубежные ученые В. С. Игнатовский, Д. Р. Карсон, Б. Ван-дер-Поль, А. М. Эфрос, А. М. Данилевский, К. А. Круг, А. И. Лурье и др.

М. Е. Ващенко-Захарченко показал также, что операторный метод применим не только к обыкновенным линейным дифференциальным уравнениям с постоянными коэффициентами и их системами, но также к линейным уравнениям с переменными коэффициентами и к линейным уравнениям с постоянными коэффициентами в частных производных, т. е., говоря на языке электротехники, к расчету переходных процессов в цепях с распределенными параметрами.

Сущность операторного метода заключается в том, что некоторой заданной однозначной ограниченной функции f(t) действительной переменной (например, времени t), называемой оригиналом, удовлетворяющей условиям Дирихле на любом конечном промежутке времени и равной нулю при t<0, сопоставляется другая функция F(p) комплексного переменного , называемая изображением.

Это сопоставление производится по формуле

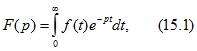
которая представляет собой прямое преобразование Лапласа функции а(t) и обозначается так:

где F(р) называется лапласовым изображением функции f(t).

Обратно: если нужно по имеющемуся изображению F (р) найти оригинал f(t), то это может быть выполнено в общем случае при помощи обратного преобразования Лапласа (интеграла Бромвича)

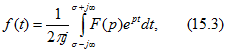
которое представляет собой решение интегрального уравнения (15.1) относительно неизвестной функции f(t) и может быть получено методами теории функций комплексного переменного. Интеграл (15.3) вычисляется по прямой на плоскости комплексного переменного , параллельной мнимой оси и расположенной правее всех особенностей (в частности, простых и кратных полюсов) функции F(р).

Интеграл (15.3) обозначается еще так:

Переходные процессы описываются системой интегродифференциальных уравнений с постоянными коэффициентами. Для преобразования их по Лапласу в соответствии с (15.1) приходится находить изображения производных и интегралов от оригинала. При этом оказывается, что изображения производных и интегралов от оригинала выражаются алгебраическими функциями от изображения и от начальных значений самой функции, ее производных и интегралов. Поэтому система интегродифференциальных уравнений относительно оригиналов заменяется системой алгебраических уравнений относительно их изображений, т. е. производится алгебраи-зация исходной системы интегродифференциальных уравнений.

При решении полученной системы алгебраических уравнений определяются изображения искомых функций, а затем при помощи обратного преобразования, вытекающих из него формул или специальных таблиц - оригиналы, т. е. искомые функции времени.

Ряд таких функций и их изображений приведен в приложении 4. Подробные таблицы оригиналов и соответствующих им изображений приводятся в справочниках.

Необходимость вычисления постоянных интегрирования по начальным условиям отпадает, поскольку все начальные условия учитываются при переходе от системы интег родифференциальных уравнений к системе алгебраических уравнений.

Приведем (без вывода) формулы для изображений производных и интегралов от оригинала. Если , то

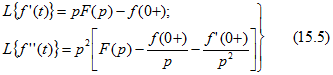
и т. д.

Отметим, что если функция f(t) и ее производные при t=0 изменяются скачком, то в (15.5) нужно подставлять их значения с учетом этих скачков, т. е. справа от нуля, что и отмечено в их аргументах знаком 0 + .

Если начальные значения функции и ее производных при t= 0+ равны нулю, то изображения первой и последующих производных находятся особенно просто:

и т. д.

Изображения интегралов от оригинала имеют вид

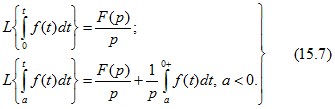
Если интеграл 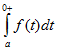при t = 0 изменяется скачком, то нужно брать его значение справа от нуля, что и обозначено в его верхнем пределе знаком 0 + .

Итак, если начальные (т. е. при t = 0 или в случае скачков при t = 0+ ) значения функции, ее производных и интегралов равны нулю, то комплексное переменное ? можно рассматривать как оператор; умножая на оператор изображение данной функции, получаем изображение ее производной (15.6), деля на оператор изображение этой функции, получаем изображение ее интеграла (15.7). В частности, изображения постоянной величины А и экспоненты соответственно равны

Нужно иметь в виду, что при расчете переходных процессов операторным методом необходимо не только находить изображения функций, их производных и интегралов, но и решать обратную задачу - находить функции (оригиналы) по их изображениям. Для этого, как указывалось, можно пользоваться таблицей из справочника.

Часто изображение имеет вид рациональной дроби

при m<n, причем дробь несократимая, т. е. многочлены общих корней не имеют, и - действительные числа.

Оригинал f(t) изображения (15.9) можно найти по формуле, называемой теоремой разложения:

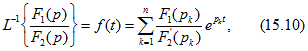
которая представляет собой сумму вычетов подынтегральной функции выражения (15.3) относительно всех ее полюсов . Здесь - простые корни характеристического уравнения , причем один из них может равняться нулю; .

Часто встречается другая форма записи разложения, применяющаяся в том случае, когда в составе знаменателя (15.9) есть множитель р, т. е. знаменатель (15.9) имеете один нулевой корень. Необходимо найти оригинал для изображения , где в составе уже нет множителя р. Предполагая, что уравнение имеет n различных и не равных нулю корней , получаем другую форму теоремы разложения:

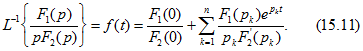
Если уравнение имеет комплексные сопряженные корни, то нет необходимости вычислять слагаемые суммы, стоящей в правых частях равенств (15.10) или (15.11) для каждого из комплексных сопряженных корней в отдельности. Известно, что функции с действительными коэффициентами от комплексных сопряженных значений независимого переменного - сами комплексные сопряженные. Поэтому если корни - комплексные и сопряженные, то достаточно вычислить слагаемое сумм (15.10) или (15.11) только для корня , а для корня взять значение, сопряженное этому слагаемому, т. е.

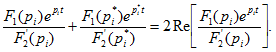
Если среди корней многочлена есть кратные, то можно записать теорему разложения аналогично формулам (15.10) или (15.11), но с двойной суммой в правой части (одна сумма - по числу корней, а вторая - для каждого корня по порядку его кратности). Однако эта формула довольно сложна и здесь не приводится.

Если изображение F (р) наряду с n простыми полюсами в точках имеет, например, еще один полюс кратности в точке , т. е.

то, применяя формулу вычета в кратном полюсе, получаем

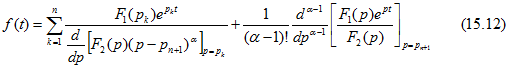
Это соотношение позволяет учесть кратные корни характеристического уравнения.

Если нужно вычислить начальное (при t = 0 + ) и установившееся (при ) значения оригинала, т.е. f(0 + ) и , то можно, конечно, пользоваться формулами (15.10) или (15.11). Однако начальное и установившееся значения оригинала в случае, если установившийся процесс непериодический, определяются гораздо проще по так называемым предельным соотношениям:

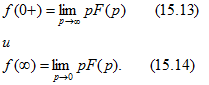
Дополнительно отметим, что теорема разложения применима не только к рациональным дробям, но и для , содержащих трансцендентные, например экспоненциальные, круговые и гиперболические функции.

Дополнительно по теме