Сопротивления

Введем теперь ряд величин, характеризующих цепь синусоидального тока.

Отношение комплексного напряжения к комплексному току называется комплексным сопротивлением:

где - отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т. е.

Комплексное сопротивление можно представить в виде

где - действительная часть комплексного сопротивления, называется активным сопротивлением; - значение мнимой части комплексного сопротивления, называется реактивным сопротивлением.

Очевидно, что

Из ( 3.23а) следует, что для последовательного контура (см. рис. 3.8) комплексное сопротивление

причем реактивное сопротивление

где

называются соответственно индуктивным и емкостным сопротивлениями.

Из ( 3.15) и ( 3.19) видно, что индуктивное сопротивление связывает между собой амплитуды или действующие значения напряжения на индуктивности и тока:

Индуктивное сопротивление прямо пропорционально частоте тока. Это объясняется тем, что напряжение на индуктивном элементе пропорционально скорости изменения тока:

Емкостное сопротивление, как следует из ( 3.16) и ( 3.20), связывает между собой амплитуды или действующие значения напряжения на емкости и тока:

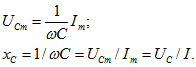
Емкостное сопротивление обратно пропорционально частоте тока. Эту зависимость от частоты легко пояснить, если считать заданным напряжение на емкостном элементе, а искомой величиной ток: . Ток прямо пропорционален скорости изменения напряжения на емкостном элементе, и, следовательно, емкостное сопротивление обратно пропорционально частоте напряжения.

Напряжения на последовательно соединенных индуктивности и емкости противоположны по фазе; поэтому в (3.27) для реактивного сопротивления х сопротивления входят с различными знаками. Напряжения на индуктивности и на емкости сдвинуты по фазе относительно напряжения на сопротивлении соответственно на p/2 и -p/2. Поэтому эти сопротивления входят в Z как .

Следует обратить внимание на то, что индуктивное и емкостное сопротивления являются величинами арифметическими - положительными, а реактивное сопротивление - величина алгебраическая и может быть как больше, так и меньше нуля.

Для ветви, содержащей только индуктивность, реактивное сопротивление х равно индуктивному сопротивлению , а реактивное сопротивление х ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т. е. .

Заметим также, что для ветвей, каждая из которых содержит только сопротивление r, только индуктивность L или только емкость С, комплексные сопротивления соответственно равны:

Если ветвь содержит несколько последовательно соединенных резистивных, индуктивных и емкостных элементов, то при вычислении сопротивления и тока их можно заменить тремя элементами:

Дополнительно по теме