Проводимости

Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению

где y=1/z - величина обратная полному сопротивлению, называется полной проводимостью.

Комплексная проводимость и комплексное сопротивление взаимно обратны. Комплексную проводимость можно представить в виде

где - действительная часть комплексной проводимости, называется активной проводимостью; - значение мнимой части комп-лексной проводимости, называется реактивной проводимостью;

Из ( 3.30) и ( 3.29) следует, что для схемы, представленной на рис. 3.12, комплексная проводимость

где

и называются соответственно активной, индуктивной и емкостной проводимостями.

Реактивная проводимость

Индуктивная и емкостная проводимости - арифметические величины, а реактивная проводимость b - алгебраическая величина и может быть как больше, так и меньше нуля. Реактивная проводимость b ветви, содержащей только индуктивность, равна индуктивной проводимости , а реактивная проводимость b ветви, содержащей только емкость, равна емкостной проводимости с обратным знаком, т. е. .

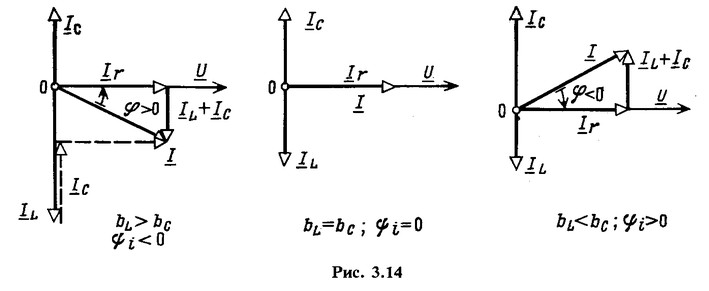
Сдвиг по фазе между напряжением и током зависит от соотношения индуктивной и емкостной проводимостей. Для схемы по рис. 3.12 на рис. 3.14 представлены векторные диаграммы для трех случаев, а именно При построении этих диаграмм начальная фаза напряжения принята равной нулю, поэтому , как это следует из ( 3.28), равны и противоположны по знаку ().

Рассматривая схему на рис. 3.12 в целом как пассивный двухполюсник, можно заметить, что при заданной частоте она эквивалентна в первом случае параллельному соединению сопротивления и индуктивности, во втором - сопротивлению и в третьем - параллельному соединению сопротивления и емкости. Второй случай называется резонансом. При заданных L и С соотношение между зависит от частоты, а поэтому от частоты зависит и вид эквивалентной схемы.

Обратим внимание на то, что в схеме рис. 3.12 каждая из параллельных ветвей содержит по одному элементу. Поэтому получилось такое простое выражение для У, в которое проводимости элементов входят как отдельные слагаемые.

Заметим, что обозначения применяются не только для сопротивлений и проводимостей, но и для элементов схемы, характеризуемых этими величинами. В таких случаях элементам схемы дают те же самые наименования, какие присвоены величинам, которые обозначаются этими буквами. Комплексные сопротивления или проводимости как элементы схемы имеют условное обозначение в виде прямоугольника (см. рис. 3.1). Точно так же обозначают реактивные сопротивления или проводимости, если хотят отметить, что они могут быть как индуктивными, так и емкостными сопротивлениями или проводимостями.

Дополнительно по теме