Разность фаз напряжения и тока

Условимся под разностью фаз j напряжения и тока всегда понимать разность начальных фаз напряжения и тока (а не наоборот):

Поэтому на векторной диаграмме угол j отсчитывается в направлении от вектора I к вектору U (рис. 3.10). Именно при таком определении разности фаз угол j равен аргументу комплексного сопротивления. Угол j положителен при отстающем токе () и отрицателен при опережающем токе ().

Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При имеем и ток отстает по фазе от напряжения, . При имеем , ток совпадает по фазе с напряжением, rLC-цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при имеем , ток опережает по фазе напряжение.

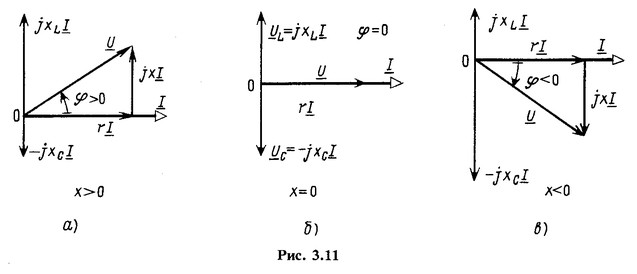
Векторные диаграммы для трех возможных соотношений даны на рис. 3.11. При построении этих диаграмм начальная фаза тока ; принята равной нулю. Поэтому равны друг другу.

Рассматривая при заданной частоте цепь по рис. 3.8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при как последовательное соединение сопротивления и индуктивности (), при как сопротивление r и при как последовательное соединение сопротивления и емкости (). При заданных L и С соотношение между зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.

Выше, в разделе, было принято, что задан ток, а определялись напряжения на элементах и на входных выводах цепи. Однако часто бывает задано напряжение на выводах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток

и тем самым действующий ток и начальную фазу тока.

Часто равной нулю принимается начальная фаза заданного напряжения: . В этом случае, как следует из раздела, начальная фаза тока ; равна и противоположна по знаку разности фаз j, т. е .

Установленные выше соотношения между амплитудами и действующими токами и напряжениями, а также выражение для сдвига фаз ф позволяют вычислить ток и не прибегая к записи закона Ома в комплексной форме. Подробно этот путь решения показан в примере 3.4.

Пример 3.4.

К цепи, состоящей из последовательно соединенных конденсатора и катушки, приложено напряжение . Емкость конденсатора С=5 мкФ, сопротивление катушки г=15 Ом, индуктивность L=12 мГн. Найти мгновенные значения тока в цепи и напряжений на конденсаторе и на катушке.

Решение.

Схема замещения цепи показана на рис. 3.8.

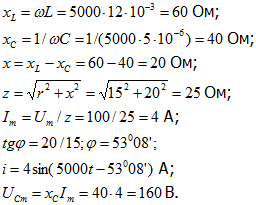
Напряжение на емкости отстает от тока по фазе на 90°, следовательно,

Комплексное сопротивление катушки

Комплексная амплитуда напряжения на выводах катушки

Мгновенное напряжение на катушке

Пример 3.5.

В цепи, состоящей из последовательно соединенных конденсатора и катушки, ток I=2 А, его частота f=50 Гц. Напряжение на выводах цепи U=100 В, катушки Uкат =150 В и конденсатора Uc=200 В. Определить сопротивление и индуктивность катушки и емкость конденсатора.

Решение.

Полное сопротивление цепи z=U/I=50 Ом.

Полное сопротивление катушки zкат=Uкат/I=75 Ом;

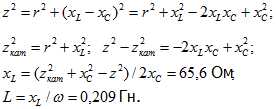
Дополнительно по теме