Баланс мощностей

Из закона сохранения энергии следует, что в любой цепи соблюдается баланс как мгновенных, так и активных мощностей. Сумма всех отдаваемых (мгновенных и активных) мощностей равна сумме всех получаемых (соответственно мгновенных или активных) мощностей. Покажем, что соблюдается баланс и для комплексных, и, следовательно, для реактивных мощностей.

Пусть общее число узлов схемы равно n. Здесь будем под узлом понимать и место соединения любых двух элементов схемы (источников и приемников), а под ветвью - каждый участок схемы, содержащий один из ее элементов.

Напишем для каждого из и узлов уравнения по первому закону Кирхгофа для комплексов, сопряженных с комплексными токами:

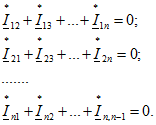
Эти уравнения записаны в общей форме в предположении, что каждый узел связан со всеми остальными n-1 узлами. При отсутствии тех или иных ветвей соответствующие слагаемые в уравнениях выпадают. При наличии между какой-либо парой узлов нескольких ветвей число слагаемых соответственно увеличивается. Так, например, если между узлами 1 и 2 включены две ветви, то вместо в уравнения войдут суммы .

Умножим каждое из уравнений на комплексный потенциал узла, для которого составлено уравнение, и затем все уравнения просуммируем. Учтем, что комплексы, сопряженные с комплексными токами, входят в эти уравнения дважды (для двух различных направлений), причем и т. д. В результате получим

т. е. сумма комплексных получаемых мощностей во всех ветвях цепи равна нулю. Здесь все слагаемые представляют комплексные получаемые мощности, потому что они вычисляются для одинаковых положительных направлений напряжений (разностей потенциалов) и токов.

Полученное равенство выражает баланс комплексных мощностей. Из него следует равенство нулю в отдельности суммы получаемых активных мощностей и суммы получаемых реактивных мощностей. Так как отрицательные получаемые мощности представляют собой мощности отдаваемые, то можно утверждать, что суммы всех отдаваемых и всех получаемых реактивных мощностей равны друг другу.

Аналогичную формулировку можно придать и балансу комплексных мощностей. Перенеся часть слагаемых в правую часть уравнения с противоположным знаком, т. е. рассматривая их как мощности отдаваемые, убедимся в равенстве сумм комплексных получаемых .и отдаваемых мощностей:

При равенстве сумм комплексных величин суммы их модулей в общем случае не равны друг другу. Отсюда следует, что для полных мощностей S баланс не соблюдается.

Получаемая пассивным двухполюсником реактивная мощность должна равняться сумме реактивных мощностей, получаемых индуктивными и емкостными элементами, которые составляют его схему:

Пользуясь соотношениями ( 3.47) и ( 3.48), получаем

Часто вместо (3.48) принимают для реактивной мощности емкостного элемента

при этом

но формула (3.49) не изменяется.

Заметим, что положения этого параграфа могут быть распространены и на цепи, между элементами которых имеются взаимные индуктивности, так как подобные цепи, как будет показано, можно свести путем преобразования к схемам, не содержащим взаимных индуктивностей.

Дополнительно по теме