Пассивный двухполюсник

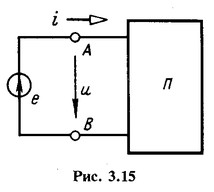
Ток и напряжение на входе любого пассивного двухполюсника (рис. 3.15) связаны законом Ома

где Z и Y - входные комплексные сопротивление и проводимость двухполюсника.

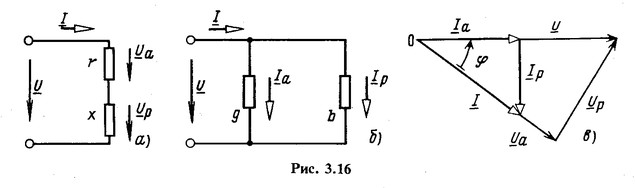
Входному комплексному сопротивлению Z=r+jx соответствует эквивалентная схема двухполюсника, состоящая из последовательного соединения активного сопротивления r и реактивного сопротивления х. Последнее в зависимости от знака следует рассматривать либо как индуктивное, либо как емкостное сопротивление. Поэтому на эквивалентной схеме (рис. 3.16, а) сопротивление х показано условно прямоугольником.

Комплексная проводимость

откуда

и наоборот

Из полученных соотношений видно, что b и х всегда имеют одинаковый знак.

Например, для схемы на рис. 3.8 получаем для g и b довольно сложные выражения, причем не только b, но и g зависят от частоты:

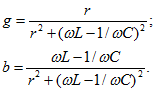
Наоборот, для схемы на рис. 3.12, состоящей из параллельного соединения элементов, получаются простые выражения для проводимостей, но относительно сложные выражения для сопротивлений, причем и эквивалентное активное сопротивление зависит от частоты. По (3.36)

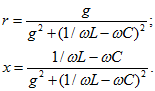
Переход от сопротивления Z = г + jx к проводимости Y = g - jb и обратно соответствует замене схемы цепи с последовательным соединением элементов r и jx эквивалентной схемой с параллельным соединением элементов g и -jb и обратно (рис. 3.16, а и б).

Напряжение U можно разложить на составляющие:

где - составляющая, совпадающая по фазе с током, называется активной составляющей напряжения; - составляющая, сдвинутая по фазе относительно тока на угол p/2, называется реактивной составляющей напряжения.

Составляющие можно рассматривать как напряжения на элементах r и х эквивалентной схемы.

На рис. 3.16, в представлена векторная диаграмма двухполюсника при j > 0, т. е. если х - индуктивное сопротивление. Треугольник, образованный векторами со сторонами, пропорциональными z, r и |х|, называется треугольником напряжений. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны сопротивлениям z, r и |х|, называется треугольником сопротивлений. Из треугольника напряжений следует, что

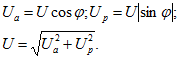
Входной комплексной проводимости Y = g - jb соответствует эквивалентная схема двухполюсника, состоящая из параллельного соединения проводимостей g и -jb. Последняя в зависимости от знака либо индуктивная, либо емкостная. Поэтому на эквивалентной схеме (рис. 3.16,6) проводимость b, показана условно прямоугольником. Ток на входе двухполюсника можно разложить на составляющие:

где - составляющая, совпадающая по фазе с напряжением, называется активной составляющей тока; - составляющая, сдвинутая по фазе относительно напряжения на угол p/2, называется реактивной составляющей тока.

Составляющие можно рассматривать как токи в элементах g и -jb эквивалентной схемы.

Треугольник, образованный векторами со сторонами, пропорциональными y, g, |b|, называется треугольником токов. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны проводимостям y, g и |b|, называется треугольником проводимостей.

Из треугольника токов имеем

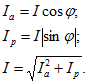
Пример 3.6.

Цепь состоит из конденсатора емкостью С = 10 мкФ и резистора с сопротивлением r - 100 Ом, включенных параллельно. Определить, каковы должны быть емкость конденсатора и сопротивление резистора, чтобы при их последовательном соединении получилась цепь, эквивалентная данной при частоте рад/с.

Решение.

Проводимости данной цепи

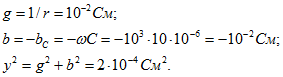
Сопротивления данной цепи

Эквивалентная цепь должна иметь такие же сопротивления. Таким образом, искомое сопротивление резистора 50 Ом, а емкость конденсатора С= - 1/wх = 20 мкФ.

Пример 3.7.

Напряжение и ток на входе пассивного двухполюсника (см. рис. 3.15)

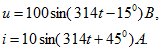
Определить параметры двух эквивалентных схем двухполюсника, активные и реактивные составляющие напряжения и тока.

Дополнительно по теме