Эквивалентные схемы четырехполюсников

Четырехполюсники эквивалентны, если при замене одного четырехполюсника другим режимы источника питания и приемника не изменяются.

Режим любого проходного четырехполюсника задается одной из систем двух уравнений (8.1)-(8.6), каждая из которых содержит в общем случае четыре независимых коэффициента. Поэтому наиболее простая эквивалентная схема или схема замещения четырехполюсника должна состоять не менее чем из четырех элементов, параметры которых зависят от коэффициентов уравнений. Для четырехполюсника, заданного одной из матриц коэффициентов, можно составить несколько эквивалентных схем, состоящих из минимально необходимого числа элементов.

Для пассивных четырехполюсников (три независимых коэффициента) чаще выбирают Т- или П-образную схему замещения (рис. 8.8, а или б), сопротивления элементов которой зависят от значений коэффициентов заданной матрицы.

Рис. 8.8

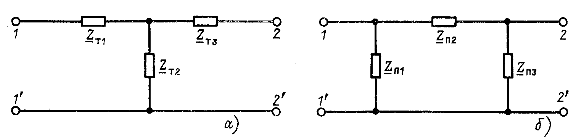
Для пассивных симметричных четырехполюсников обычно выбирают одну из трех канонических схем замещения: Т-образную (см. рис. 8.7, а), П-образную (см. рис. 8.7, б) или мостовую (рис. 8.9, а), каждая из которых задается значениями двух сопротивлений . У Т- и П-образных схем соединены накоротко выводы 1' и 2'. Такие четырехполюсники называются неуравновешенными и применяются на практике в цепях, для которых нужно иметь общую точку. К этой точке присоединяются корпуса приборов, оболочки коаксиальных кабелей, заземляющая шина и т. д. Мостовая или Х-образная схема (рис. 8.9,а) уравновешенная, у нее взаимная замена соответственно выводов 1 и 1', 2 и 2' не приводит к изменению режима в участках электрической цепи, присоединяемых к первичным и к вторичным выводам. Т- и П-образные схемы можно сделать и уравновешенными, составив продольные элементы с сопротивлением из равных частей, присоединенных так, как показано на рис. 8.9, 6 и в. Все коэффициенты уравновешенных Т- и П-образных схем такие же, как и у неуравновешенных.

Такими же расчетами, как и в примере 8.4, сопротивления можно выразить через коэффициенты уравнений любого типа. Например, для мостовой схемы (рис. 8.9, а) получается

Симметрию относительно первичных и вторичных выводов называют еще симметрией относительно поперечной оси (мысленно проведенной вертикально через центр на рис. 8.7 - 8.9). Уравновешенные четырехполюсники называют еще симметричными относительно продольной оси (горизонтальной, проведенной через центр на рис. 8.9).

Рис. 8.9

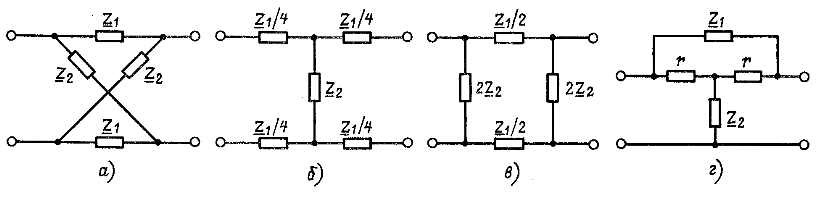
Мостовая схема выбирается как основная для предварительного проектирования (синтеза) симметричных четырехполюсников; Т-, П-образные и мостовые схемы, состоящие из резистивных элементов, применяются для изменения уровня сигналов и называются аттенюаторами или удлинителями.

Симметричные перекрытые Т-образные четырехполюсники (рис. 8.9, г) применяются в качестве амплитудных корректоров, т. е. четырехполюсников, которые включаются в цепь передачи сигналов для требуемого изменения ее амплитудно-частотной характеристики.

Управляемые (зависимые) источники напряжения и тока. В предыдущих главах при анализе электрических цепей было принято, что идеальные и реальные источники напряжения (ЭДС) и тока задаются не зависящими от режима цепи параметрами ( в цепи постоянного тока или в цепи синусоидального тока). Только при пояснении принципов компенсации и эквивалентного генератора (теоремы об активном двухполюснике) было введено понятие о простейшем зависимом источнике - двухполюснике, ЭДС которого зависит от тока двухполюсника.

При исследовании цепей с многополюсниками, в частности с четырехполюсниками, содержащими, например, транзисторы, гираторы, идеальные трансформаторы, операционные усилители, нельзя построить эквивалентную схему, состоящую только из резистивных, индуктивных, емкостных элементов и идеальных или реальных источников напряжения и тока с постоянными параметрами. Для построения эквивалентных схем дополнительно нужно ввести управляемые (зависимые) источники.

Управляемый источник - это элемент с двумя парами выводов (входной и выходной), т. е. четырехполюсник. Он содержит идеальный источник напряжения (ЭДС) или тока, который управляется напряжением между какими-либо двумя выводами цепи или током в какой-либо ветви.

Рис. 8.10

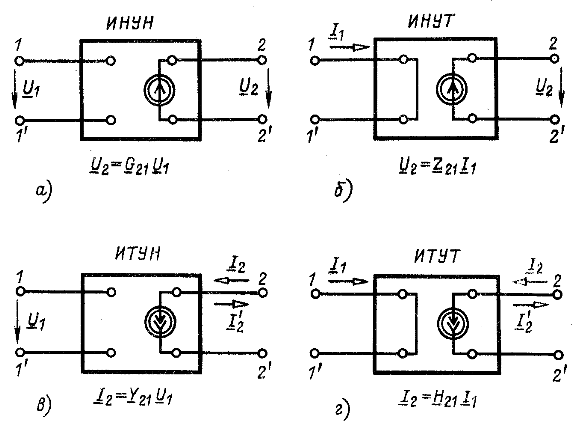
Различают четыре типа управляемых источников, у которых выходная величина не влияет на входную:

источник напряжения, управляемый напряжением (ИНУН, рис. 8.10, а), с матрицами коэффициентов четырехполюсника

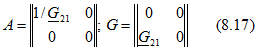
и напряжением на выходных выводах, пропорциональным напряжению на выводах, которые рассматриваются как входные;
источник напряжения, управляемый током (ИНУТ, рис. 8.10,6), с матрицами

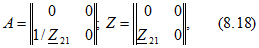
т. е. с напряжением на выходных выводах, зависящим от тока ветви, которая считается входной у четырехполюсника;
источник тока, управляемый напряжением (ИТУН, рис. 8.10, в), с матрицами

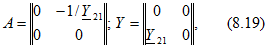
т. е. выходной ток является заданной функцией напряжения на входных выводах ;
источник тока, управляемый током (ИТУТ, рис. 8.10, г), с матрицами

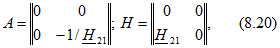
т. е. выходной ток пропорционален входному.

Другие матрицы у таких четырехполюсников не существуют, и их следует рассматривать как частного вида активные неавтономные четырехполюсники. Управляемые источники напряжения и тока применяются, например, при построении эквивалентных схем устройств с транзисторами. Так, в эквивалентной схеме однокаскадного усилителя (см. рис. 8.6) есть ИТУТ, у которого ток источника пропорционален току базы .

Для активного неавтономного четырехполюсника две простейшие схемы замещения общего вида получаются добавлением к Т- или П-образной схеме (см. рис. 8.8) четвертого элемента - управляемого (зависимого) источника напряжения (ЭДС) или тока (рис. 8.11, а и б). Возможны и другие схемы замещения, одна из которых показана на рис. 8.11, в.

Рис. 8.11

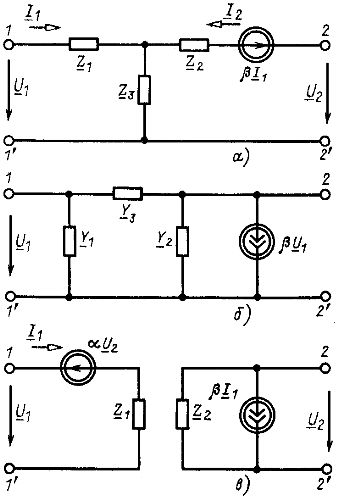
Пример 8.5. Выразить параметры элементов схемы замещения по рис. 8.11, а через коэффициенты матрицы Z.

Решение. Запишем уравнения для двух контуров схемы по рис. 8.11, а:

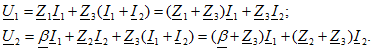
Сравнивая составленные уравнения с (8.3), находим

откуда определяем искомые параметры

Параметры схемы на рис. 8.11,6 проще всего определяются через коэффициенты матрицы Y, а схемы на рис. 8.11, в - через коэффициенты матрицы Н. В результате получается для схемы на рис. 8.11, б

и для схемы на рис. 8.11, в

При составлении схем замещения некоторые резистивные сопротивления могут получиться и отрицательными, как и при замене схемы соединения треугольником эквивалентным соединением звездой (см. раздел). Такие сопротивления не препятствуют расчету режима четырехполюсника, но в реальной цепи должны быть заменены источниками.

Гиратор или инвертор сопротивления.

К активным невзаимным четырехполюсникам частного вида относится гиратор - четырехполюсник, который задается любой из следующих четырех матриц:

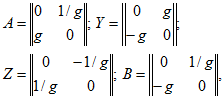
где g - действительная величина, называемая коэффициентом гирации. Матрицы G и Н не существуют. Это невзаимный четырехполюсник, так как

Условное графическое изображение гиратора показано на рис. 8.12, а.

Для практического осуществления гиратор требует применения двух управляемых источников. На рис. 8.12,6 представлена эквивалентная схема с двумя управляемыми источниками тока, на рис. 8.12, в -с двумя управляемыми источниками напряжения.

Из любой системы уравнений гиратора можно определить его входное сопротивление

т. е. входное сопротивление инвертора пропорционально проводимости нагрузки. Важно отметить, что при емкостном сопротивлении получается входное индуктивное сопротивление , т.е. можно реализовать индуктивный элемент при помощи активного четырехполюсника и емкостного элемента (и наоборот). Гиратор выпускается в интегральном исполнении как один из элементов электрических цепей.

Возможно построение инверторов сопротивления и с другими параметрами, например вместо .

Конвертор сопротивления. Как и инвертор сопротивления, конвертор - это активный неавтономный четырехполюсник. Он задается, например, матрицей

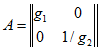
и

его входное сопротивление пропорционально сопротивлению нагрузки. При действительных коэффициентах , отрицательном значении одного из них и резистивном сопротивлении нагрузки входное сопротивление , т. е. получается резистивный элемент с отрицательным сопротивлением. Как и для гиратора, реализация требует применения управляемых источников (рис. 8.12, г).

Рис. 8.12

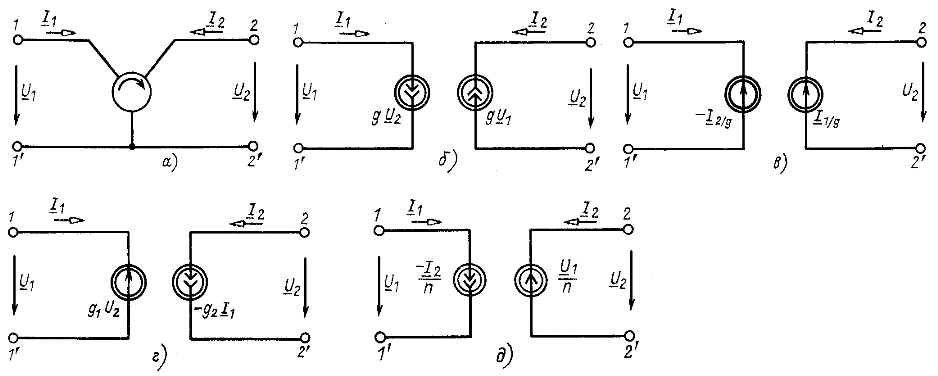
Идеальный трансформатор. Управляемые источники содержит схема замещения идеального трансформатора: ИТУТ в первичной цепи и ИНУН во вторичной (рис. 8.12, д). Такое представление трансформатора требуется, например, для электронных устройств с микросхемами (интегральная технология).

Дополнительно по теме