Характеристические (вторичные) параметры пассивных четырехполюсников

Довольно часто на практике между источником питания (генератором) и приемником бывает включена цепь, состоящая из нескольких четырехполюсников, а в самом простом случае включается один симметричный пассивный четырехполюсник. Например, индивидуальная телевизионная приемная антенна (источник сигналов для телевизора) присоединяется к телевизору (приемник сигналов) не непосредственно, а при помощи симметричного четырехполюсника - телевизионного кабеля. Отрезок кабеля имеет два входных вывода 1-1', которыми он соединен с источником питания (антенна), и два выходных вывода 2-2', к которым присоединяется приемник (телевизор). Очень важно правильно выбрать сопротивление приемника . Его выбирают так, чтобы входное сопротивление четырехполюсника - кабеля на выводах 1-1' было одинаковым и равным независимо от длины кабеля. При одинаковых входных сопротивлениях кабелей разной длины все генераторы - антенны, к которым присоединены кабели, оказываются одинаково нагруженными. Следовательно, конструкция всех антенн может быть одинаковой независимо от длины кабеля.

Аналогичные задачи правильного выбора сопротивления нагрузки возникают и в других установках с четырехполюсниками - аттенюаторами, цепными схемами, фильтрами и т. д.

Поставим вопрос о том, как же надо нагрузить симметричный четырехполюсник, чтобы его входное сопротивление равнялось сопротивлению нагрузки?

У симметричного четырехполюсника любую пару выводов (1-1' или 2-2') можно принять за входную, при этом режимы источника питания и приемника не изменяются. Предположим для определенности, что источник питания присоединен к первичным выводам 1-1' (см. рис. 8.2, а). Найдем входное сопротивление по (8.7а), учитывая, что для симметричного четырехполюсника

Необходимо иметь , т. е. должно быть

Последнее выражение определяет значение сопротивления нагрузки , при котором и входное сопротивление равно сопротивлению нагрузки. Преобразовав последнее выражение, найдем, что

Итак, если выбрать вполне определенное сопротивление приемника, а именно равное , то и входное сопротивление четырехполюсника равно этому значению. Входное сопротивление четырехполюсника при такой нагрузке зависит только от его коэффициентов и, значит, может быть принято одним из параметров четырехполюсника (как и коэффициенты уравнений любого типа).

Новый параметр нужно знать, если возникает задача о выборе нагрузки для готового четырехполюсника или, наоборот, если проектируют четырехполюсник для совместной работы с заданным приемником.

Этот параметр обозначают и называют характеристическим сопротивлением симметричного четырехполюсника:

Рис. 8.13

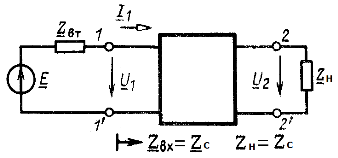
Режим четырехполюсника при называют режимом согласованной нагрузки. Если у источника питания нужно учитывать внутреннее сопротивление (рис. 8.13) и оно равно , то и источник питания считают согласованным с четырехполюсником. В режиме согласования источника

Этот режим совпадает с режимом максимальной активной мощности источника только при резистивных сопротивлениях источника питания и приемника.

В качестве второго параметра симметричного четырехполюсника выбирают величину, которая позволяет весьма просто сравнивать напряжения и токи на входе и выходе четырехполюсника при согласованной нагрузке.

Для сравнения напряжений на входе и выходе составим их соотношение при согласованной нагрузке

где - модуль отношения, характеризует изменение значения напряжения; - аргумент отношения (радиан или градусов), показывает сдвиг фаз между напряжениями на входе и выходе. Этот угол называется (собственной или характеристической) постоянной фазы.

Комплексную величину не следует путать с передаточной функцией по напряжению , которая определяется при любой заданной нагрузке четырехполюсника. Передаточную функцию нельзя считать параметром четырехполюсника, так как ее модуль и аргумент зависят от сопротивления приемника. Комплексная величина определяется обязательно при согласованной нагрузке, т. е. при сопротивлении нагрузки, равном одному из параметров четырехполюсника - характеристическому сопротивлению. Поэтому комплексная величина - параметр четырехполюсника. В случае согласованной нагрузки

Напряжение на выходе четырехполюсника нередко значительно отличается от значения напряжения на входе. Например, на выходе фильтра радиоприемника напряжение на частоте принимаемого сигнала может практически равняться напряжению на входе а на частоте другого сигнала быть в тысячи раз меньше. Поэтому отношение напряжений на входе и выходе принято оценивать в логарифмическом масштабе, для чего вместо отношения напряжений т вводится (собственная или характеристическая) постоянная ослабления

или

Постоянная ослабления - физическая безразмерная величина. Поэтому ее единицей измерения служит непер (Нп). Постоянной ослабления А = 1 Нп обладает четырехполюсник, у которого при согласованной нагрузке напряжение на выходе в раза меньше, чем на входе.

При согласованной нагрузке

Следовательно,

и постоянная ослабления характеризует как отношение напряжений, так и отношение токов на входных и выходных выводах:

а постоянная фазы В - сдвиг по фазе между токами, который равен сдвигу фаз между напряжениями.

Постоянную ослабления можно вычислить и по известным полным или активным мощностям на входе и выходе. Действительно,

или

так как сдвиг фаз между напряжением и током на входе и на выходе один и тот же .

Запишем выражение (8.24) с постоянной ослабления А

откуда

Комплексная безразмерная величина характеризует изменение напряжения и тока при согласованной нагрузке как по значению, так и по фазе и называется (собственной или характеристической) постоянной передачи четырехполюсника. Постоянная передачи - второй параметр симметричного четырехполюсника.

Постоянная передачи в (8.30) выражена через напряжения и токи на входе и выходе четырехполюсника, но она, как и характеристическое сопротивление, полностью определяется структурой четырехполюсника и параметрами составляющих его элементов. Постоянную передачи, как и , можно, например, определить через коэффициенты матрицы А.

По (8.30) с учетом согласованной нагрузки и (8.22)

или

так как у симметричного четырехполюсника

Характеристическое сопротивление и постоянную передачи называют вторичными параметрами симметричного четырехполюсника.

Постоянную ослабления часто вычисляют не через натуральный логарифм, а через десятичный в децибелах:

Не следует забывать, что при вычислении постоянной передачи по формуле следует подставлять значение А в неперах и В в радианах.

Уравнения с гиперболическими функциями.

Вторичные параметры - характеристическое сопротивление и постоянная передачи - полностью определяют симметричный пассивный четырехполюсник как устройство, входящее в тракт передачи и преобразования сигналов. Поэтому такой четырехполюсник часто задается вторичными параметрами. В этом случае при исследовании режима целесообразно пользоваться уравнениями, в которых напряжения и токи связаны между собой при помощи вторичных параметров.

Чтобы составить такие уравнения, выразим коэффициенты матрицы А через вторичные параметры и подставим в (8.1а). Из (8.31) следует, что

Кроме того, известно уравнение связи коэффициентов или для симметричного четырехполюсника , что дает после деления на (8.32)

Решив уравнения (8.32) и (8.33) относительно , получим

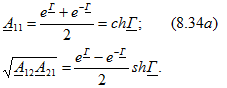
Умножив и разделив последнее выражение на , найдем, что

Наконец, подставив (8.34) в (8.1а), получим уравнения симметричного четырехполюсника с гиперболическими функциями

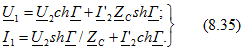
Входное сопротивление симметричного пассивного четырехполюсника

В частности, при коротком замыкании

и при холостом ходе

Из (8.36) определяем вторичные параметры:

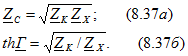
Несимметричные пассивные четырехполюсники определяются тремя независимыми коэффициентами любого типа уравнений. Поэтому и вторичных параметров у пассивного несимметричного четырехполюсника три: характеристическое сопротивление со стороны первичных выводов , характеристическое сопротивление со стороны вторичных выводов и постоянная передачи .

Рис. 8.14

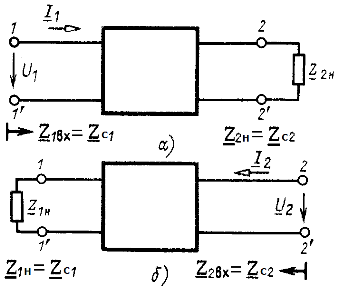
Характеристическое сопротивление равно такому сопротивлению приемника , подключенного к вторичным выводам, при котором входное сопротивление со стороны первичных выводов равно (рис. 8.14, а). Короче говоря, при имеем . Аналогично при обратном питании и сопротивлении приемника на первичных выводах получим (рис. 8.14, 6).

Постоянную передачи определим при питании со стороны первичных выводов

и постоянная ослабления

Они не могут быть выражены только через напряжения или только через токи, как у симметричного четырехполюсника. Точно так же постоянная фазы В не показывает сдвиг фаз между напряжениями или между токами.

Хотя четырехполюсник и несимметричен, постоянная передачи при питании со стороны вторичных выводов (и согласованной нагрузке на первичных) равна постоянной передачи при питании со стороны первичных выводов (и согласованной нагрузке на вторичных). Это можно показать на основании принципа взаимности.

Связь между вторичными параметрами и коэффициентами матрицы А (или другими коэффициентами) сложнее, чем у симметричного четырехполюсника. Расчеты, аналогичные приведенным в разделе, дают следующие зависимости:

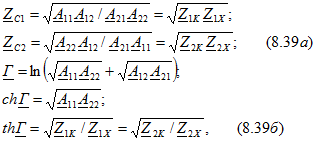
откуда можно получить значения коэффициентов уравнений типа А и записать уравнения с гиперболическими функциями, подставив найденные значения в (8.1а).

Постоянной ослабления можно дать и другое толкование. Предположим, что требуется выяснить, какую полную мощность получил бы приемник с сопротивлением от заданного источника питания при непосредственном подключении приемника к заданному источнику (рис. 8.15, а) с выполнением условия согласования источника

Рис. 8.15

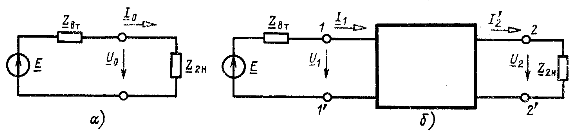
Напряжение и ток приемника в схеме на рис. 8.15, а при

Эти напряжение и ток получаются такими же, как и напряжение и ток на входе четырехполюсника при согласованной нагрузке на вторичных выводах и согласованном источнике, т. е. , а именно . Поэтому

и постоянная ослабления

Дополнительно по теме