Четырехполюсники и многополюсники
Ранее были рассмотрены общие методы расчета линейных электрических цепей, например методы наложения, контурных токов, узловых потенциалов. Применив эти методы, можно найти режим работы любой линейной цепи.
Однако во многих случаях анализа и синтеза электрических цепей важно знать токи только некоторых ветвей и напряжения только между некоторыми узлами. В этом случае расчет цепи упрощается, если цепь разделить на отдельные части, каждая из которых соединена с остальной двумя, тремя, четырьмя или большим числом выводов - полюсов. Так, например, при определении режима в одной единственной ветви всю остальную часть цепи можно рассматривать как двухполюсник. При расчете методом преобразования иногда полезно выделить треугольник сопротивлений, т. е. трехполюсник, который можно заменить трехлучевой звездой сопротивлений (также трехполюсником). Анализ сложных электрических цепей нередко можно выполнить проще, если выделить многополюсники.
В различных областях электротехники особенно часто применяются аппараты и устройства с двумя парами выводов, при помощи которых они соединяются с другими участками электрической цепи, т. е. четырехполюсники.
На практике четырехполюсники и цепи, которые целесообразно представить состоящими из нескольких четырехполюсников, применяются прежде всего для передачи и преобразования электрических сигналов, несущих информацию. Тракт передачи информации, или канал связи, как правило, состоит из ряда четырехполюсников, включенных между генератором (передатчиком) сигналов и приемником сигналов. B тракт передачи обычно входят:
- линия связи генератора и приемника, находящихся часто на значительных расстояниях один от другого;
- усилители, в которых увеличивается мощность или, как говорят, уровень сигналов;
- аттенюаторы (ослабители) для снижения уровня сигналов;
- фильтры для разделения сигналов;
- корректирующие контуры, включаемые для устранения искажений сигналов;
- трансформаторы, при помощи которых изменяются сопротивления отдельных участков тракта передачи информации и устраняется гальваническая связь между этими участками.
К четырехполюсникам относятся также некоторые цепи обратной связи электронных генераторов и усилителей, участки линий передачи электрической (электромагнитной) энергии, цепи регулирования различных параметров машин (скорости, давления, напряжения) и т. д.
Таким образом, теория четырехполюсников дает возможность единым методом анализировать системы, самые различные по структуре и принципу действия. Кроме того, сложная цепь расчленяется на более простые части, характеристики которых дают полное представление о режиме работы всей цепи.
Условное изображение четырехполюсника показано на рис. 8.1. Одну пару выводов из четырех (четырех полюсов) назовем первичной, а другую - вторичной и обозначим соответственно цифрами 1-1' и 2-2'. Для расчета режима выберем положительные направления напряжений и токов, показанные на рис. 8.1.
Рис. 8.1
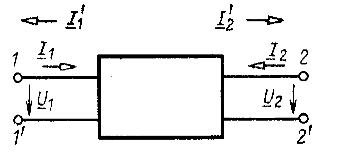
Будем считать, что источники питания, приемники, двухполюсники, четырехполюсники и вообще любые участки цепи с парными выводами могут присоединяться только к выводам четырехполюсника, которые обозначены одинаковыми цифрами. Такие четырехполюсники называют проходными.
Все четырехполюсники подразделяются еще на две группы: пассивные и активные. В пассивных четырехполюсниках нет зависимых или независимых источников напряжения (ЭДС) или тока, активные четырехполюсники содержат зависимые или независимые источники. Пассивными четырехполюсниками являются, например, линии передачи сигналов, трансформаторы, аттенюаторы, корректирующие контуры. К активным относятся усилители, собранные на транзисторах или электронных лампах, в том числе операционные усилители, лампы бегущей волны и др.
Активные четырехполюсники, содержащие только зависимые источники, называются неавтономными, а включающие и независимые источники, - автономными. Для пассивных проходных четырехполюсников выполняется принцип взаимности. Поэтому они называются обратимыми. Для активных четырехполюсников принцип взаимности выполняется только в частном случае.
Далее предполагается, что напряжения и токи источников питания, которые могут подключаться к выводам 1-1' и 2-2', а значит, и напряжения, и токи на всех участках цепи синусоидальные.
На практике устройства, которые анализируются как четырехполюсники, чаще работают в цепях несинусоидального тока, хотя могут быть и в цепях синусоидального, и в цепях постоянного токов. Для применения рассматриваемой здесь теории к цепям несинусоидального тока необходимо исследовать частотные зависимости параметров четырехполюсников. Все расчетные формулы и соотношения могут быть отнесены и к цепям постоянного тока, если положить частоту равной нулю.
Для исследования четырехполюсников необходимо прежде всего установить зависимости между четырьмя величинами, определяющими режим его работы: напряжениями и токами на первичных и вторичных выводах.
Рассмотрим сначала режимы работы неавтономных активных и пассивных проходных четырехполюсников.
Зависимости между двумя напряжениями и двумя токами, определяющими режим на первичных и вторичных выводах, могут быть записаны в различной форме. Если считать две из указанных величин заданными, то две другие величины будут связаны с ними системой двух уравнений, которые называются уравнениями четырехполюсника.
Рис. 8.2
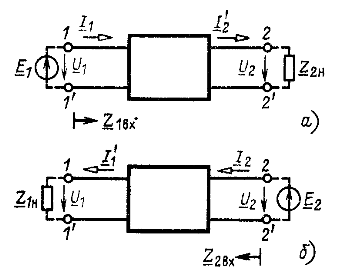
Например, если к вторичным выводам четырехполюсника подключен приемник с сопротивлением нагрузки ![]() , а к первичным - источник ЭДС
, а к первичным - источник ЭДС ![]() (рис. 8.2, а), то при заданном напряжении на выводах приемника
(рис. 8.2, а), то при заданном напряжении на выводах приемника ![]() (в частности, при номинальном напряжении приемника) и токе
(в частности, при номинальном напряжении приемника) и токе ![]() можно определить необходимое напряжение источника питания на первичных выводах
можно определить необходимое напряжение источника питания на первичных выводах ![]() и ток источника
и ток источника ![]() по уравнениям типа А:
по уравнениям типа А:
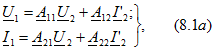
или в матричной форме
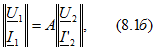
где 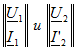 - матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах;
- матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах;
![]() - квадратная матрица коэффициентов.
- квадратная матрица коэффициентов.
В этих уравнениях коэффициенты ![]() определяют сам четырехполюсник и зависят от схемы соединения и параметров составляющего четырехполюсник элементов электрической цепи;
определяют сам четырехполюсник и зависят от схемы соединения и параметров составляющего четырехполюсник элементов электрической цепи; ![]() - безразмерные коэффициенты;
- безразмерные коэффициенты; ![]() имеет размерность сопротивления, а
имеет размерность сопротивления, а ![]() - проводимости.
- проводимости.
Всего можно записать шесть различных по форме, но по существу эквивалентных, т. е. математически равносильных, пар уравнений (число сочетаний из четырех по два).
Уравнения типа Y
![]()
или
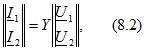
где все коэффициенты - проводимости.
Уравнения типа Z
![]()
или
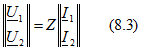
с коэффициентами - сопротивлениями.
Уравнения типа Н
![]()
или
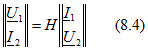
с коэффициентами, размерность которых, как и в первых трех системах уравнений, непосредственно следует из самой записи уравнений.
Уравнения типа G
![]()
или
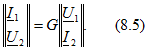
Уравнения типа В
![]()
или
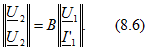
Дополнительно по теме
- Режимы четырехполюсников
- Коэффициенты четырехполюсников
- Эквивалентные схемы четырехполюсников
- Характеристические (вторичные) параметры пассивных четырехполюсников
- Цепные схемы
- Эксплуатационные параметры четырехполюсников Активные автономные четырехполюсники
- Многополюсники
- Операционный усилитель
- Обратная связь

