Комплексные частотные характеристики
Смотри примеры расчета:
Последовательное соединение приемников
Параллельное соединение приемников
Смешанное соединение приемников
Дуальность электрических цепей
Комплексные частотные характеристики
Комплексные частотные характеристики
К частотным характеристикам цепи в комплексной форме, или к комплексным частотным характеристикам, относятся входные и передаточные функции, записанные в комплексной форме.
Входная комплексная функция цепи - это зависимость от частоты комплексного сопротивления
или комплексной проводимости
относительно двух выделенных или заданных выводов.
В качестве примера построим зависимости от частоты модуля 
и аргумента 
входного комплексного сопротивления параллельной схемы замещения реального конденсатора с заданными параметрами g и С, считая их в рассматриваемом диапазоне частот неизменными.
Входное сопротивление
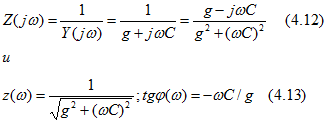
Зависимости 
показаны на рис. 4.16, а и б.
Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме. Предполагается, что в цепи действует одно внешнее воздействие, т. е. цепь содержит один источник воздействия, а другие независимые источники напряжения или тока отсутствуют или не действуют.
Различают четыре вида передаточных функций:
передаточная функция по напряжению
передаточная функция по току
передаточное сопротивление
передаточная проводимость
Передаточные функции
могут определяться для различных пар выбранных входных и выходных выводов цепи.
В частном случае обе пары выводов совпадают, так что 
, т. е. для них получается тривиальное решение. Зависимость модуля передаточной функции K(w) от частоты называется амплитудно - частотной характеристикой (АЧХ), зависи мость аргумента передаiочной функции y(w) - фазо-частотной характеристикой (ФЧХ). На комплексной плоскости можно построить геометрическое место конца вектора К(jw) при изменении частоты - амплитудно - фазовую характеристику (АФХ), или годограф вектора К(jw).
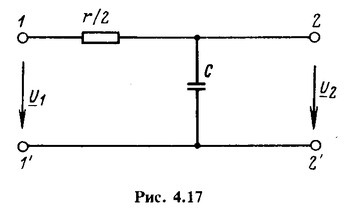В качестве примера определим АЧХ и ФЧХ передаточной функции по напряжению простейшего rС-фильтра, схема которого дана на рис. 4.17, в режиме холостого хода. Входные выводы фильтра 1-1', т.е. 
выходные выводы 2-2', т. е. 
.
Передаточная функция
т. е. амплитудно-частотная и фазо-частотная характеристики
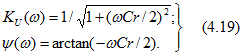
Зависимости (4.19) аналогичны (4.13), т.е. графики 
такие же, как и на рис. 4.16, но с 
.
Для пепей с сосредоточенными параметрами передаточная функция может быть представлена в виде отношения двух полиномов относительно р=jw с действительными коэффициентами:
Если К(jw) - безразмерная величина 
, то можно составить логарифмическую амплитудно-фазовую характеристику
В (4.20) единице действительной составляющей логарифмической АФХ, т. е. безразмерной логарифмической амплитудной характеристике, 
дано название непер (Нп), мнимая составляющая y(w) должна быть записана в радианах. Для логарифмической амплитудной характеристики применяют и другую единицу - децибел (дБ). В этом случае вычисляется 
. Непер и децибел связаны соотношением 
.
Смотри примеры расчета:
Последовательное соединение приемников
Параллельное соединение приемников
Смешанное соединение приемников