Резонанс в индуктивно связанных контурах

В устройствах электроники и радиотехники наряду с одиночными последовательными и параллельными контурами применяются и связанные контуры. Контуры могут иметь индуктивную связь (трансформаторную или автотрансформаторную) или емкостную различного вида.

Рис. 6.18

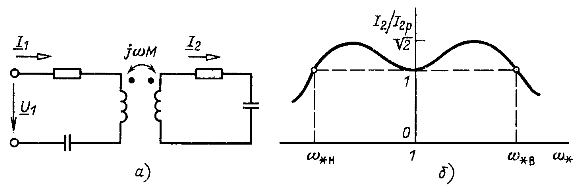
Рассмотрим резонансные явления для случая двух одинаковых последовательных контуров (в целях упрощения математического описания), имеющих индуктивную (трансформаторную) связь (рис. 6.18, а). Режим цени определяется двумя уравнениями:

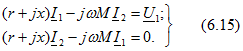
где

При частоте у каждого контура x=0 (каждый настроен в резонанс) - так называемый "полный резонанс". Из (6.15) следует, что ток , т. е. совпадает по фазе с напряжением и цепь настроена в резонанс. Ток

При любой другой частоте из (6.15) ток

В относительных единицах

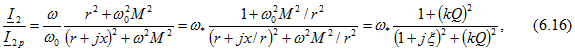
так как . Здесь - относительная частота; Q - добротность каждого из контуров; - коэффициент связи и

- обобщенная расстройка.

В (6.16) принято, что при построении резонансной кривой контура с достаточно большой добротностью можно принять множитель и при вычислении добротности Q считать . Это, конечно, справедливо при достаточно малых расстройках (например, при x =3 и Q=20 получается ). Резонансная кривая

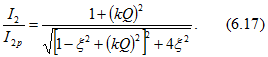
Если kQ<<1 - слабая связь контуров, то

Резонансная кривая имеет один максимум при x = 0, т. е. при . Ток меньше в раз (границы полосы пропускания) при , а у последовательного контура [см. формулу 5.5] и на границах полосы пропускания . Следовательно, полоса пропускания связанных контуров при слабой связи меньше, чем у последовательного контура.

При kQ = 1 - критической связи и на границах полосы пропускания , т. е. полоса пропускания больше, чем у последовательного контура.

При kQ > 1 - сильной связи получается резонансная кривая с двумя максимумами (рис. 6.18, б). Если считать, что на границе полосы пропускания значение тока , как и у последовательного контура, в раз меньше максимального, то получится полоса пропускания в 3,1 раза шире и ближе к прямоугольной, чем у последовательного контура при той же добротности контуров, что может быть важным достоинством цепи при построении систем с большой полосой пропускания (широкополосных).

Значение тока зависит от коэффициента связи контуров. Наибольшее значение можно найти обычным исследованием на максимум. Оно получается при и .

Аналогично исследуются "частные резонансы". Первый частный резонанс достигается изменением емкости (или индуктивности) первого контура.

При резонансе и ток совпадает по фазе с напряжением . Для получения второго частного резонанса добиваются максимального значения тока изменением емкости (или индуктивности) второго контура. "Сложный резонанс" получается при изменении параметров одного из контуров и коэффициента связи.

Дополнительно по теме