Расчеты разветвленных цепей при наличии взаимной индуктивности
Расчеты разветвленных цепей можно вести, составляя уравнения по первому и второму законам Кирхгофа или методом контурных токов. Метод узловых потенциалов непосредственно непригоден. Объясняется это тем, что ток в любой ветви зависит не только от ЭДС находящегося в ней источника и от потенциалов тех узлов, к которым ветвь присоединена, но и от токов других ветвей, которые наводят ЭДС взаимной индукции. Поэтому нельзя простым путем выразить токи ветвей через потенциалы узлов и ЭДС источников, как в цепях без индуктивно связанных элементов.
Применение метода узловых потенциалов требует особых приемов и здесь не рассматривается.
Принцип эквивалентного генератора можно применять, если внешняя по отношению к двухполюснику часть цепи не имеет индуктивных связей с той частью цепи, которая входит в состав двухполюсника. Разумеется, что нельзя пользоваться выведенными ранее формулами для преобразования треугольника сопротивлений в эквивалентную звезду и обратно.
Чтобы обойти указанные выше ограничения в применении расчетных методов, в ряде случаев целесообразно исключить индуктивные связи, перейдя к эквивалентным схемам без индуктивных связей.
При составлении уравнения по второму закону Кирхгофа ЭДС взаимной индукции обычно учитываются как соответствующие напряжения. Знак комплексного напряжения ![]() на элементе k определяется на основании сопоставления направления обхода элемента к и положительного направления тока в элементе s. Если эти направления относительно одноименных выводов одинаковы, то напряжение равно
на элементе k определяется на основании сопоставления направления обхода элемента к и положительного направления тока в элементе s. Если эти направления относительно одноименных выводов одинаковы, то напряжение равно ![]() . В противном случае напряжение равно
. В противном случае напряжение равно ![]() . Это правило знаков вытекает из обоснований, приведенных в разделе Индуктивно связанные элементы цепи.
. Это правило знаков вытекает из обоснований, приведенных в разделе Индуктивно связанные элементы цепи.
Рис. 6.10
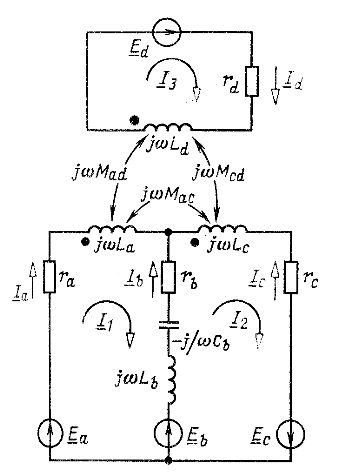
В качестве примера запишем уравнения по законам Кирхгофа для схемы, представленной на рис. 6.10. Для большей ясности напряжения в уравнениях выпишем в порядке расположения элементов контура без приведения подобных членов:
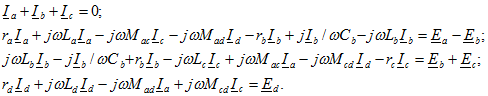
Приведем также уравнения, составленные по второму закону Кирхгофа для контурных токов:
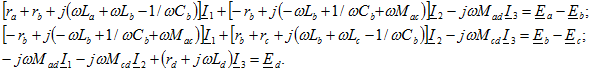
Сокращенно последние уравнения можно записать так:
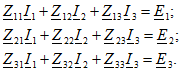
где ![]() - комплексные сопротивления контуров 1, 2 и 3;
- комплексные сопротивления контуров 1, 2 и 3;
![]() - комплексные взаимные (общие) сопротивления контуров 1 и 2, 2 и 3, 3 и 1;
- комплексные взаимные (общие) сопротивления контуров 1 и 2, 2 и 3, 3 и 1; ![]() - комплексные контурные ЭДС. Например,
- комплексные контурные ЭДС. Например,
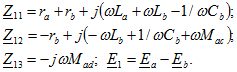
Заметим, что в комплексные сопротивления контуров и в комплексные взаимные сопротивления двух контуров слагаемые ![]() входят со знаком плюс или минус в зависимости от того, совпадают или не совпадают по отношению к одноименным выводам элементов цепи k и s направление обхода контура через элемент к и положительное направление тока через элемент s.
входят со знаком плюс или минус в зависимости от того, совпадают или не совпадают по отношению к одноименным выводам элементов цепи k и s направление обхода контура через элемент к и положительное направление тока через элемент s.
Для цепей, содержащих индуктивно связанные элементы, справедливо свойство взаимности. Доказательство этого положения ничем не отличается от приведенного для цепей постоянного тока.
Пример 6.1.
К выводам 1-1' цепи (рис. 6.11) подведено питание. Определить напряжение между разомкнутыми выводами 2-2'. Дано: ![]()
Рис. 6.11
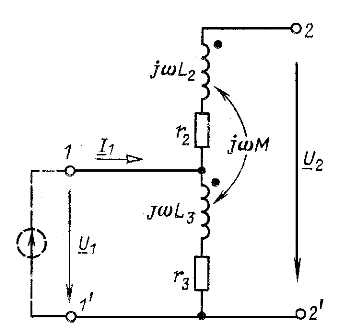
Решение. Полагаем ![]() . Находим:
. Находим:
![]()
Напряжение ![]() определяем, обходя схему от вывода 2 к выводу 2':
определяем, обходя схему от вывода 2 к выводу 2':
![]()
Если бы нижний вывод индуктивности ![]() был одноименным с верхним выводом индуктивности
был одноименным с верхним выводом индуктивности ![]() , то направление обхода элемента
, то направление обхода элемента ![]() и направление тока в элементе
и направление тока в элементе ![]() относительно одноименных выводов были бы различными. Поэтому перед слагаемым
относительно одноименных выводов были бы различными. Поэтому перед слагаемым ![]() следовало бы поставить знак минус, и напряжение
следовало бы поставить знак минус, и напряжение ![]() было бы равно
было бы равно ![]() .
.
Пример 6.2.
Определить входное сопротивление цепи, показанной на рис. 6.12. Дано: ![]() .
.
Рис. 6.12
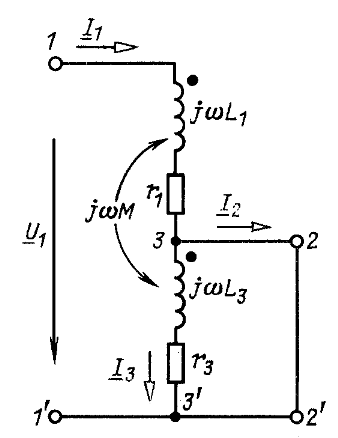
Решение. Зададимся напряжением ![]() определим ток
определим ток ![]() и затем найдем
и затем найдем ![]() . Заметим, что если бы не было взаимной индуктивности, то
. Заметим, что если бы не было взаимной индуктивности, то ![]() .
.
Для контура 1-3-2-2'-1'
![]()
Для контура 3-3'-2'-2-3
![]()
откуда
![]()
Подставив (в) в (а), получим
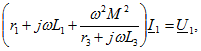
откуда
![]()
Дополнительно по теме
- Электродвижущая сила взаимной индукции
- Последовательное соединение индуктивно связанных элементов цепи
- Параллельное соединение индуктивно связанных элементов цепи
- Эквивалентная замена индуктивных связей
- Передача энергии между индуктивно связанными элементами цепи
- Резонанс в индуктивно связанных контурах

