Резонансные явления при изменении параметров контура
Резонансные явления при изменении параметров контура
Как было указано в разделе, резонанса можно достичь не только изменением частоты напряжения питания, но и изменением индуктивности или емкости. Практически контур настраивают в резонанс чаще при помощи конденсатора переменной емкости.
Предположим, что у последовательного контура (см. рис. 3.8) емкость изменяется. Рассчитаем и построим резонансные кривые тока и напряжений на индуктивности и емкости. Ток
![]()
равен нулю при С = О, растет с увеличением емкости до резонансного значения ![]() при
при ![]() (рис. 5.4, а), удовлетворяющего условию резонанса
(рис. 5.4, а), удовлетворяющего условию резонанса ![]() , затем уменьшается при дальнейшем увеличении емкости и стремится к значению
, затем уменьшается при дальнейшем увеличении емкости и стремится к значению
![]() при
при ![]() .
.
Добротность контура, как и ранее ( 5.4), равна отношению индуктивного или равного ему емкостного сопротивления при резонансе к активному сопротивлению контура:
![]()
Напряжение на индуктивности ![]() , т. е. форма кривой
, т. е. форма кривой ![]() такая же, как и
такая же, как и ![]() . Максимальное значение
. Максимальное значение ![]() . При
. При ![]() напряжение
напряжение ![]() (рис. 5.4,6).
(рис. 5.4,6).
Дополнительно по теме
- Вынужденные и свободные колебания
- Резонанс в последовательном контуре
- Частотные характеристики и резонансные кривые последовательного контура
- Резонансные явления при изменении параметров контура
- Резонанс в параллельном контуре
- Частотные характеристики параллельного контура
- Понятие о резонансе в сложных цепях
Рис. 5.4
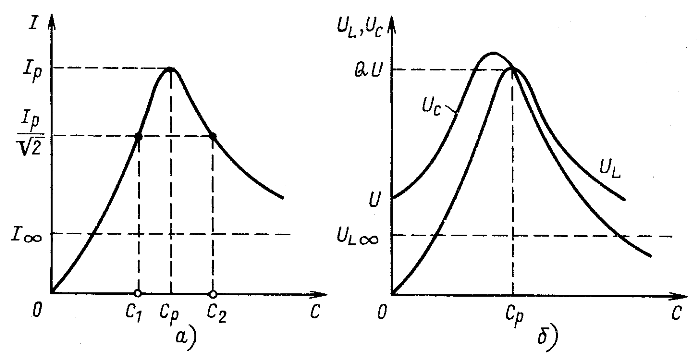
Напряжение на емкости ![]() при С = 0, достигает максимального значения при
при С = 0, достигает максимального значения при ![]() (если Q > 1), равно
(если Q > 1), равно ![]() при
при ![]() и стремится к нулю при
и стремится к нулю при ![]() (рис. 5.4, б). При Q > 10 с погрешностью менее 1 % можно считать, что максимальное значение напряжения на емкости получается при
(рис. 5.4, б). При Q > 10 с погрешностью менее 1 % можно считать, что максимальное значение напряжения на емкости получается при ![]() , т. е. равно QU.
, т. е. равно QU.
Измерив значения емкостей ![]() и
и ![]() , при которых ток в
, при которых ток в ![]() раз меньше резонансного, можно рассчитать параметры контура: r, L, Q. Для этого перепишем (5.6) в виде
раз меньше резонансного, можно рассчитать параметры контура: r, L, Q. Для этого перепишем (5.6) в виде
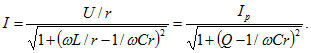
При ![]() и
и ![]() подкоренное выражение равно 2, т. е.
подкоренное выражение равно 2, т. е. ![]() или
или
![]()
После вычитания из второго условия (5.8) первого получим ![]() , откуда
, откуда
![]()
Сложив первое и второе условия (5.8), найдем, что ![]() , откуда после подстановки (5.8) добротность
, откуда после подстановки (5.8) добротность
![]()
Индуктивность определяем из (5.7):
![]()
Дополнительно по теме
- Вынужденные и свободные колебания
- Резонанс в последовательном контуре
- Частотные характеристики и резонансные кривые последовательного контура
- Резонансные явления при изменении параметров контура
- Резонанс в параллельном контуре
- Частотные характеристики параллельного контура
- Понятие о резонансе в сложных цепях

