Понятие о резонансе в сложных цепях

Условия фазового резонанса b=0 или x=0 для разветвленной цепи с несколькими катушками индуктивности и конденсаторами дают для частоты w уравнения, которые могут иметь несколько действительных корней. Другими словами, у разветвленной цепи может быть несколько резонансных частот.

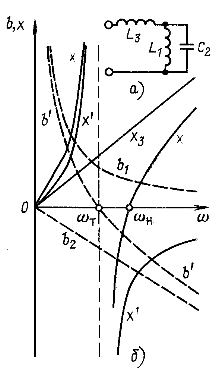
Рассмотрим, например, цепь на рис. 5.9, а, потерями в которой можно пренебречь. Входное сопротивление цепи реактивное:

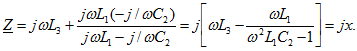
Резонанс наступает при b=0 или x=0, причем если x=0, то , и, наоборот, если b=0, то . Это справедливо всегда, если пренебречь потерями в ветвях. Следовательно, резонансными будут частоты, обращающие x в нуль или в бесконечность. В рассматриваемом случае при или

При этой частоте наступает резонанс токов в параллельных ветвях с и . Полагая x=0, получаем

При этой частоте имеет место резонанс напряжений в последовательном контуре с индуктивностью и емкостью, эквивалентной двум параллельным ветвям. Таким образом, у рассматриваемой цепи две резонансные частоты: и .

На рис. 5.9, б приведены частотные характеристики проводимостей и сопротивлений для рассматриваемой цепи. Кривые и представляют характеристики проводимостей ветвей 1 и 2. Суммируя ординаты этих кривых, получаем характеристику эквивалентной проводимости b' двух параллельных ветвей 1 и 2. Кривая х'=1/b' представляет эквивалентное сопротивление параллельных ветвей. Суммируя ординаты кривых х' и , построим характеристику входного сопротивления цепи х. Эта характеристика имеет две особые точки при (резонанс токов) и (резонанс напряжений).

Дополнительно по теме

Рис. 5.9