Смешанное соединение приемников
Смешанное соединение приемников
Токи в цепях со смешанным соединением приемников проще всего рассчитываются путем преобразования схем или методом подобия (методом пропорциональных величин). Ниже иллюстрируется первый метод. Второй метод поясняется на странице.
Пусть заданы сопротивления всех элементов схемы (рис. 4.3) и напряжение U на ее входе; требуется определить токи во всех ветвях.
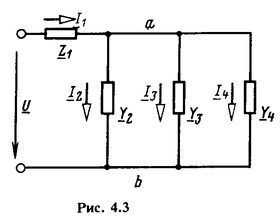
Заменим параллельно соединенные приемники энергии одним эквивалентным с проводимостью Y'=Y2+Y3+Y4 или сопротивлением Z'=1/Y'. После этого преобразования схема состоит из двух последовательно соединенных сопротивлений Z1 и Z'. Ее общее или эквивалентное сопротивление Z=Z1+Z'.
Ток в неразветвленной части цепи I1=U/Z- Напряжение на разветвлении U'=Z'I1. Токи в параллельно соединенных приемниках I2=U'/Z2; I3=U'/Z3; I4=U'/Z4.
На практике встречаются задачи и по расчету параметров цепи, удовлетворяющих различным поставленным условиям.
Смотри примеры расчета:
Последовательное соединение приемников
Параллельное соединение приемников
Смешанное соединение приемников
Дуальность электрических цепей
Комплексные частотные характеристики
Пример 4.5.
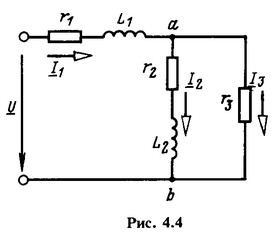
Даны сопротивления (рис. 4.4) Z1 = 200 + j1000 Ом и Z2 = 500 + j1500 Ом. Определить, при каком сопротивлении r3 ток I2 отстает по фазе от напряжения U на угол p/2.
Решение.
Сначала наметим ход решения.
Положим начальную фазу напряжения U равной нулю, т. е. U=U. Затем методом, указанным в начале параграфа, найдем в общем виде выражение для тока I2. Этот ток будет отставать по фазе на p/2 от напряжения U=U в том случае, если комплекс I2 будет отрицательной мнимой величиной. Это и является условием для определения сопротивления r3.
В соответствии с намеченным планом решения находим эквивалентное сопротивление цепи
ток в неразветвленной части цепи
напряжение на разветвлении
и, наконец, ток
Числитель этого выражения - действительная величина. Комплекс I2 будет отрицательным мнимым, если знаменатель - положительный мнимый, т. е. при условии 700r3 - 1 400000 = 0 или при r3 = 2000 Ом.
К расчету цепи со смешанным соединением приводит решение многих практически важных задач, в частности получение максимальной мощности приемником, составление условий равновесия моста переменного тока.
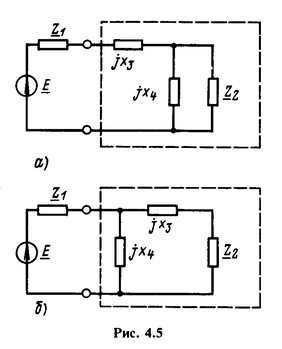Определим реактивные сопротивления X3 и X4 (рис. 4.5, а и б), при которых приемник с сопротивлением Z2=r2 + jx2 получает максимальную мощность от источника с внутренним сопротивлением Z1=r1 + jx1.
Вся активная мощность, отдаваемая источником, потребляется в приемнике (в сопротивлении r2), так как остальные сопротивления - реактивные. Поэтому необходимо, чтобы входное сопротивление каждого пассивного двухполюсника (на рис. 4.5 обведены штриховой линией) было равно сопряженному комплексному внутреннему сопротивлению источника 
т. е. для схемы рис. 4.5, а нужно, чтобы
и для схемы рис. 4.5, б
Каждое из полученных уравнений для комплексных величин можно записать в виде двух уравнений - для действительных и для мнимых величин, из которых и определяются X3 и X4.
Реальные элементы цепи обладают не только реактивными, но и активными сопротивлениями, поэтому приведенный расчет согласования сопротивлений приемника и источника питания является приближенным.
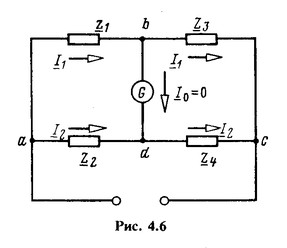Найдем соотношение между сопротивлениями Z1, Z2, Z3 и Z4 мостовой схемы (рис. 4.6), при выполнении которого мост находится в равновесии, т. е. ток I0 в диагонали моста равен нулю.
Заметим, что в качестве индикатора, по которому судят об отсутствии тока в диагонали моста, применяют телефон, вибрационный гальванометр и различные электронные приборы.
Ток в диагонали моста отсутствует, если Ubd=0, т. е. при Z1I1=Z2I2 и Z3I1=Z4I2.
Разделив эти равенства друг на друга, имеем Z1/Z3=Z2/Z4, или
или
Зная три комплексных сопротивления, при которых наблюдается равновесие моста, можно определить четвертое.
Смотри примеры расчета:
Последовательное соединение приемников
Параллельное соединение приемников
Смешанное соединение приемников
Дуальность электрических цепей
Комплексные частотные характеристики