Определение ориентации координатных осей, осей эллипса рассеяния и построение эллипса
Определение ориентации координатных осей, осей эллипса рассеяния и построение эллипса
ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ КООРДИНАТНЫХ ОСЕЙ, ОСЕЙ ЭЛЛИПСА РАССЕЯНИЯ И ПОСТРОЕНИЕ ЭЛЛИПСА
Выше было показано, что координаты ЦЭН ![]() можно в силу ряда причин рассматривать как случайные величины, подчиняющиеся нормальному закону распределения, причем было принято допущение о независимости этих координат. В связи с этим оси эллипса рассеяния строились параллельно осям координат. В общем случае координаты ЦЭН следует рассматривать как зависимые величины.
можно в силу ряда причин рассматривать как случайные величины, подчиняющиеся нормальному закону распределения, причем было принято допущение о независимости этих координат. В связи с этим оси эллипса рассеяния строились параллельно осям координат. В общем случае координаты ЦЭН следует рассматривать как зависимые величины.
Известно, что для связанных случайных величин характерна вероятностная («стохастическая») зависимость, которая может быть более или менее тесной. Эта зависимость определяется коэффициентом корреляции, причем последний характеризует степень тесноты линейной вероятностной связи. В теории вероятностей доказывается, что две независимые случайные величины всегда являются некоррелированными, однако из некоррелированности случайных величин не всегда следует их независимость.
Если известен ряд значений пары чисел ![]() то эмпирический, т.е. полученный на основании экспериментальных данных, коэффициент корреляции можно определить по следующей формуле:
то эмпирический, т.е. полученный на основании экспериментальных данных, коэффициент корреляции можно определить по следующей формуле: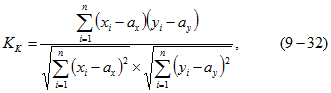 где n — количество пар чисел статистической совокупности
где n — количество пар чисел статистической совокупности ![]() ;
; ![]() — эмпирические математические ожидания, определяемые из выражения ( 9-21).
— эмпирические математические ожидания, определяемые из выражения ( 9-21).
В общем случае коэффициент корреляции может иметь значения в пределах![]() Исходя из этих соображений, можно сказать, что оси эллипса рассеяния образуют с осями координат некоторый угол
Исходя из этих соображений, можно сказать, что оси эллипса рассеяния образуют с осями координат некоторый угол ![]() , который определяется следующим образом:
, который определяется следующим образом: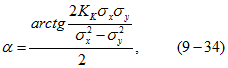 где
где ![]() — эмпирические дисперсии, определяемые из выражения ( 9-22).
— эмпирические дисперсии, определяемые из выражения ( 9-22).
Следовательно, для ориентации осей эллипса рассеяния необходимо по формуле (9-34) найти угол ![]() , который составляют оси эллипса рассеяния с осью абсцисс произвольно взятой системы координат. Угол
, который составляют оси эллипса рассеяния с осью абсцисс произвольно взятой системы координат. Угол ![]() может быть положительным или отрицательным в зависимости от выбранного положения осей координат, величина его находится в прямой зависимости от коэффициента корреляции.
может быть положительным или отрицательным в зависимости от выбранного положения осей координат, величина его находится в прямой зависимости от коэффициента корреляции.
Необходимо заметить, что коэффициент корреляции не изменяется при изменениях начала отсчета и масштаба измерения случайных величин. Обычно при выборе координатных осей стараются заранее сориентировать координатные оси так, чтобы они примерно совпали с осями симметрии эллипса рассеяния. В этом случае нормальный закон распределения будет определяться выражением ( 9-14), а его числовые характеристики — формулами (9-21)—(9-23).
В тех случаях, когда это сделать заранее невозможно, для построения эллипса рассеяния начало координат необходимо перенести в точку ![]() , а координатные оси повернуть на угол
, а координатные оси повернуть на угол ![]() , определяемый выражением (9-34). При этом нормальный закон распределения в новой системе координат
, определяемый выражением (9-34). При этом нормальный закон распределения в новой системе координат ![]() будет иметь вид:
будет иметь вид: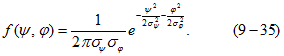 Величины
Величины ![]() выражаются через среднеквадратичные отклонения в прежней системе координат формулами
выражаются через среднеквадратичные отклонения в прежней системе координат формулами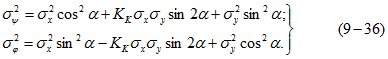 Полуоси эллипса определяются в этом случае следующим образом:
Полуоси эллипса определяются в этом случае следующим образом: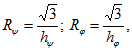 где
где![]()
Пример 9-2. Для промышленного предприятия, генплан которого приведен на рис. 9-4, построить зону рассеяния ЦЭН (рис. 9-5). Исходные данные (координаты, м; мощность, кВт):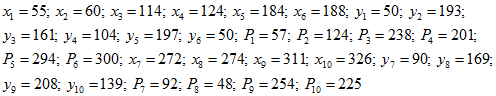 Для сокращения объема примера суточные графики электрических нагрузок не приводится.
Для сокращения объема примера суточные графики электрических нагрузок не приводится.
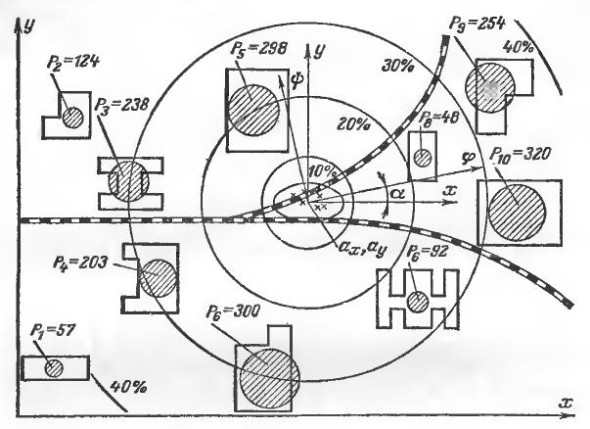
Рис. 9-4. Генеральный план предприятия с зоной рассеяния при некоррелированных величинах х и у с учетом корреляции (![]() ). Угол
). Угол ![]() дан для найденного коэффициента корреляции.
дан для найденного коэффициента корреляции.
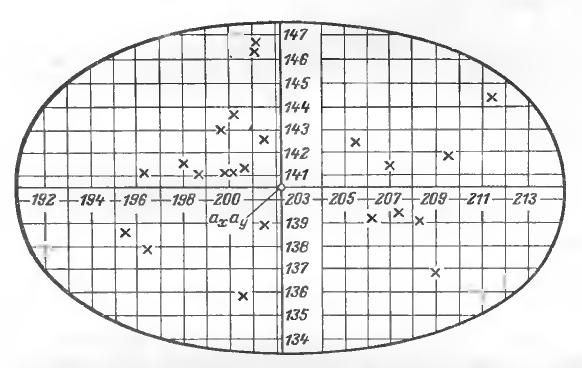
Рис. 9-5. Зона рассеяния центра электрических активных нагрузок одного из промышленных предприятии.
1. Определяем координаты ЦЭН в соответствии с суточным графиком электрических нагрузок по формуле ( 9-2):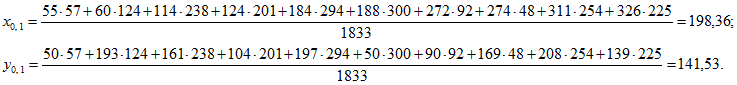 Остальные точки находятся аналогично.
Остальные точки находятся аналогично.
2. Определяем параметры нормальною закона распределения по выражениям (9-21) и (9-23):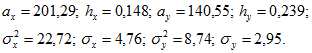 3. Определяем полуоси эллипса рассеяния по формуле (9-31):
3. Определяем полуоси эллипса рассеяния по формуле (9-31):![]() 4. Прежде чем перейти к построению зоны рассеяния ЦЭН, необходимо определить коэффициент корреляции и угол
4. Прежде чем перейти к построению зоны рассеяния ЦЭН, необходимо определить коэффициент корреляции и угол ![]() в соответствии с формулами (9-32) и (9-34);
в соответствии с формулами (9-32) и (9-34);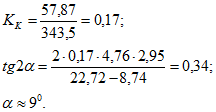 5. Определяем параметры нормального закона распределения в побои системе координат по формулам (9-36), (9-37):
5. Определяем параметры нормального закона распределения в побои системе координат по формулам (9-36), (9-37):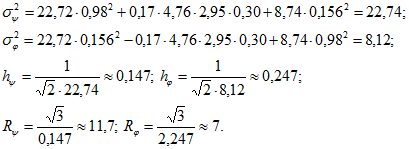 Таким образом, из приведенного расчета видно, что оси координат сориентированы так, что коэффициент корреляции и угол
Таким образом, из приведенного расчета видно, что оси координат сориентированы так, что коэффициент корреляции и угол ![]() получаются незначительными.
получаются незначительными.
Величины ![]() практически не меняются.
практически не меняются.
Для построения зоны рассеяния в данном случае достаточно перенести оси координат параллельно самим себе в точку ![]() и по осям х и у отложить соответственно величины
и по осям х и у отложить соответственно величины ![]() . Для сравнения на рис. 9-4 нанесен эллипс рассеяния с учетом коэффициента корреляции.
. Для сравнения на рис. 9-4 нанесен эллипс рассеяния с учетом коэффициента корреляции.
Смотри еще по разделу:
Картограмма нагрузок
Определение условного центра электрических нагрузок
Определение зоны рассеяния центра электрических нагрузок для статического состояния системы электроснабжения промышленных предприятий
Определение ориентации координатных осей, осей эллипса рассеяния и построение эллипса
Определение зон увеличения приведенных расчетных годовых затрат при смещении подстанции из зоны рассеяния центра электрических нагрузок
Определение местоположения ГПП (ГРП) с учетом динамики (развития) систем электроснабжения промышленных предприятий
Определение местоположения питающих подстанции во всех трех осях координат
Влияние зон рассеяния центров электрических нагрузок (ЦЭН) цехов на зону рассеяния ЦЭН промышленного предприятия
Характерные схемы электроснабжения промышленных предприятий

