Определение местоположения питающих подстанции во всех трех осях координат

ОПРЕДЕЛЕНИЕ МЕСТОПОЛОЖЕНИЯ ПИТАЮЩИХ ПОДСТАНЦИИ ВО ВСЕХ ТРЕХ ОСЯХ КООРДИНАТ

Такое определение необходимо для высотных сооружений или для подстанций подземного исполнения (шахты, рудники и т. п.).
Особое значение имеет определение рационального местоположения питающих подстанций для предприятий, которые находятся под землей (шахты, рудники и т. д.). В этом случае неправильное размещение подстанций довольно значительно сказывается на экономических показателях системы электроснабжения.
Для рационального размещения питающих подстанций на территории подобного рода предприятий необходимо определить зону рассеяния центра электрических нагрузок. В этих случаях необходимо учитывать третью координату, которая характеризует глубину залегания подземных разработок. Порядок определения зоны рассеяния ЦЭН следующий. Находится условный ЦЭН предприятия не только на поверхности, но и с учетом третьей координаты, т. е.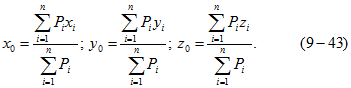 Исследованиями установлено, что распределение случайных координат ЦЭН и в этом случае следует нормальному закону распределения. Главная особенность, выделяющая нормальный закон среди других, состоит в том, что он является предельным законом, к которому приближаются законы распределения.
Плотности распределения вероятностей случайных координат х, y, z можно записать при помощи следующих выражений: Считая, что случайные координаты независимы, а начало координат совмещено с точкой, определяемой математическими ожиданиями, используется следующая формула для трехмерной (объемной) плотности распределения случайных координат: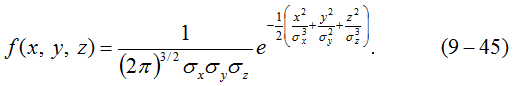 После нахождения закона распределения случайных координат ЦЭН можно непосредственно переходить к решению задачи определения зоны рассеяния ЦЭН предприятия подземного типа. Для этого необходимо определить значения величин, характеризующих функцию трехмерной плотности нормального распределения. После этого определяются форма, геометрические размеры и местоположение зоны рассеяния.
Эмпирические числовые характеристики найденного закона распределения (математическое ожидание и дисперсия) определяются из следующих выражений: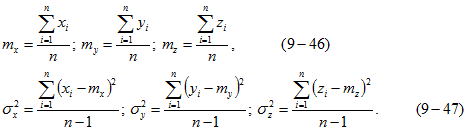 Рассмотрим формулу (9-45), определяющую форму зоны, в которой случайные координаты распределяются с одинаковой плотностью, т. е. так называемую зону рассеяния ЦЭН. Для этого, приняв объемную плотность распределения за некоторое постоянное значение, т. е. и прологарифмировав выражение (9-45), получим: где Формула (9-49) представляет собой уравнение эллипсоида в каноническом виде. В этом случае полуоси эллипсоида соответственно равны: Таким образом, зоной рассеяния ЦЭН является эллипсоид с осями, параллельными осям координат, и центром, определяемым математическими ожиданиями.
Вероятность попадания случайных координат х, у, z внутрь данного К-эллипсоида равна: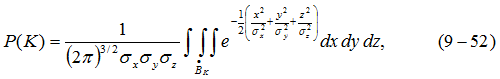 где Вк — объем, ограниченный К-эллипсоидом.
Перейдя к сферической системе координат и проинтегрировав по частям выражение (9-52), получим: где — лапласиан вида

Приняв в качестве доверительной вероятности, т. е. вероятности, при которой попадание случайных величин в зону, ограниченную данным эллипсоидом, считается практически достоверным, величину Р(К)=0,95, получим: Изложенные положения справедливы при допущении, что случайные величины независимы и тогда ориентация главных осей рассеяния эллипсоида заранее известна и все преобразования производятся в системе координат, оси которой параллельны главным осям рассеяния. Поскольку на практике не всегда можно определить ориентацию главных осей рассеяния даже приблизительно, рассмотрим случай, когда случайные величины х, у, z коррелированы и направление главных осей рассеяния заранее неизвестно. В этом случае рекомендуется следующий порядок решения задачи:
1. Произвольно выбирается ориентация и положение координатных осей.
2. Производится расчет, в котором не учитывается зависимость между величинами х, у, z.
а) определяются координатх, у, z;
б) производится перенос начала координат в точку, определяемую величинами ;
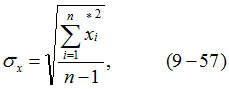
в) осуществляется расчет случайных величин х, у, z в связи с переносом осей по следующим формулам: Определяются величин : определяются аналогично.
3. Производится расчет с учетом зависимости между случайными величинами :

а) коэффициента корреляции между этими величинами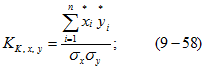 б) угла поворота вокруг оси: в) параметров и числовых характеристик новой системы координат по следующим формулам: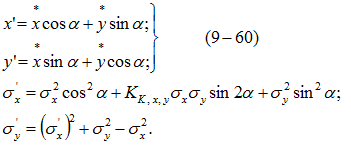 4. Производится расчет с учетом зависимости между случайными величинами .
а) коэффициента корреляции между случайными величинами 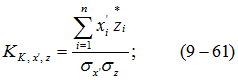б) угла поворота вокрут оси y'

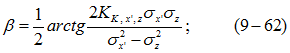
в) параметров и числовых характеристик новой системы координат по следующим формулам: 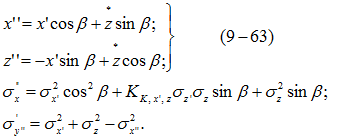5. Производится расчет с учетом зависимости между случайными величинами у' и z":
а) коэффициента корреляции между у' и z"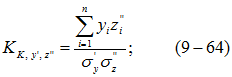 б) угла поворота вокруг оси х" в) параметров и числовых характеристик новой системы координат х'', y''', z"':

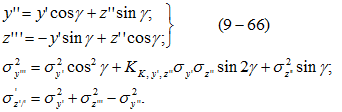
Поскольку ориентация осей x"', y"', z''' определена из условий, что случайные величины x"', y"', z''' попарно независимы, полученные оси будут являться главными осями рассеяния. Определение полуосей эллипсоида, представляющего собой зону рассеяния ЦЭН, производится в соответствии со следующим выражением: Эллипсоид рассекается плоскостями, что соответствует уровню какого-либо горизонта, и в сечении получается эллипс, в котором целесообразно размещать подстанцию. Уравнение эллипса при z=С имеет вид: Обозначив получим полуоси эллипса Если х, у значительно больше z, можно пренебречь корреляционной зависимостью z, х и z, у.
Для производства расчетов по указанной выше методике применяются ЭВМ.
Таким образом, для промышленных предприятий, которые размещаются под землей, зоной рассеяния ЦЭН является эллипсоид. Для рационального расположения питающих подстанций предприятий указанного типа необходимо размещать их внутри эллипсоида, что обеспечивает минимальные годовые приведенные затраты и, следовательно, является экономически целесообразным.