Высшие гармоники в трехфазных цепях

В трехфазных цепях кривые напряжения во второй и третьей фазах со сдвигом на треть периода обычно в точности воспроизводят форму кривой напряжения в первой фазе. Так, например, если напряжение в фазе А может быть представлено некоторой функцией времени , то , где Т-период основной частоты.

Рассмотрим гармонику порядка k функции во всех трех фазах. Пусть .

Учитывая, что и подставляя вместо t соответственно t - Т/3 и t + T/3, получаем .

Сравнивая полученные выражения для различных значений k, можно заметить, что напряжения гармоник порядка, кратного трем (k=3n), где n - любое целое число, во всех фазах в любой момент времени имеют одно и то же значение и направление. При k= 3n+1 гармоники трех фаз образуют симметричную систему напряжений, последовательность которой совпадает с последовательностью фаз 1-й гармоники. При k=3n+2 гармоники образуют симметричную систему напряжений с последовательностью, обратной основной.

Таким образом, гармоники порядка 1, 4, 7, 10, 13 и т. д. образуют системы напряжений прямой последовательности, гармоники 2, 5, 8, 11, 14 и т. д. образуют системы напряжений обратной последовательности. Наконец, гармоники 3, 6, 9, 12 и т. д. образуют системы напряжений нулевой последовательности. При наличии постоянной составляющей в напряжении каждой из фаз она может рассматриваться как нулевая гармоника порядка, кратного трем (k=0), т. е. образующая нулевую последовательность.

В большинстве практически важных случаев в напряжениях отсутствуют как постоянная составляющая, так и все четные гармоники, поэтому в дальнейшем ограничимся исследованием только нечетных гармоник.

Различные схемы соединения трехфазных цепей

Если фазы генератора соединены звездой, то при несинусоидальном фазном напряжении линейные напряжения, равные разностям напряжений двух смежных фаз, не содержат гармоник напряжений порядка, кратного трем, так как последние образуют системы нулевой последовательности.

Отсутствие гармоник порядка, кратного трем, в линейных напряжениях приводит к тому, что при несинусоидальных напряжениях отношение линейного напряжения к фазному меньше . Действительно, фазное напряжение

а линейное напряжение

Отсюда следует, что

При симметричной нагрузке фазные токи основной частоты и все высшие гармоники, за исключением высших гармоник порядка, кратного трем, образуют системы прямой и обратной последовательностей и дают в сумме нуль. Гармоники же порядка, кратного трем, образуют систему нулевой последовательности, т. е. имеют в любой момент времени одинаковые значения и направления. Поэтому ток в нейтральном проводе равен утроенной сумме токов высших гармоник нулевой последовательности:

При отсутствии нейтрального провода токи в каждой из фаз не могут содержать высших гармоник порядка, кратного трем, так как в этой схеме сумма токов в любой момент времени должна равняться нулю, что невозможно при наличии высших гармоник порядка, кратного трем. Поэтому в приемнике нет напряжений от токов нулевой последовательности и между нейтральными точками генератора и симметричного приемника может появиться значительное напряжение, содержащее только гармоники, кратные трем.

Если фазы генератора соединены треугольником, то при несинусоидальных ЭДС в фазах сумма ЭДС, действующих в замкнутом контуре генератора, не равна нулю, как при синусоидальных ЭДС, а равна тройной сумме высших гармоник порядка, кратного трем. Если включить вольтметр в рассечку треугольника (рис. 12.21), то вольтметр измерит гармоники ЭДС порядка, кратного трем, так как остальные в сумме дадут нуль, т. е.

Рис. 12.21

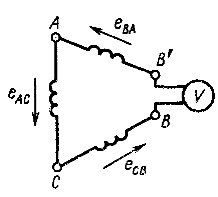
Открытый треугольник с ЭДС, содержащими высшие гармоники, применяется как утроитель частоты.

Если фазы соединены в замкнутый треугольник, то ЭДС гармоник порядка, кратного трем, вызывают внутренний ток в генераторе. Этот ток протекает в замкнутом треугольнике генератора даже и в режиме холостого хода генератора. Составляющая фазной ЭДС, содержащая гармоники порядка, кратного трем, однако, не выявляется между выводами фаз, так как она компенсируется падением напряжения на внутреннем сопротивлении фазы генератора. Фазное напряжение, равное в данном случае линейному,

Поэтому во внешней цепи, подключенной к генератору, обмотки которого соединены треугольником, токи не содержат гармоник порядка, кратного трем.

Фазный ток генератора при симметричной нагрузке

а линейный ток во внешней цепи

Пример 12.12.

Найти показания приборов при разомкнутом и замкнутом ключе

Найти показания приборов при разомкнутом и замкнутом ключе S в трехфазной цени (рис. 12.22, а), имеющей соединенную звездой трехфазную систему источников (вторичные обмотки трехфазного трансформатора) с фазными ЭДС (в вольтах):

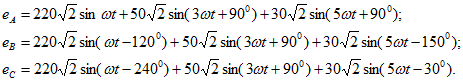
Сопротивление источника для 1-й гармоники . Приемником служат три конденсатора, соединенных звездой. Для 1-й гармоники .

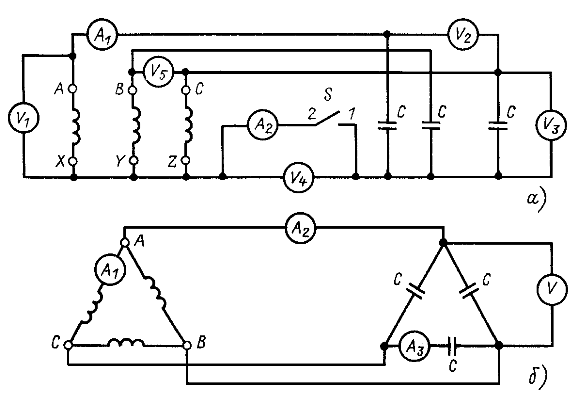
Рис. 12.22

Решение. Найдем показания приборов (индексы токов и напряжений соответствуют обозначениям приборов в схеме).

Для случая звезды без нейтрального провода (ключ S разомкнут)

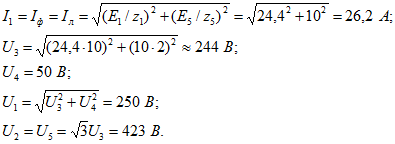
Для случая звезды с нейтральным проводом (ключ S замкнут)

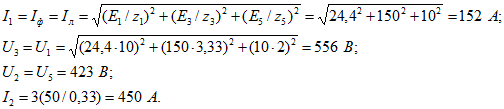
Близость к резонансу на 3-й гармонике привела к очень большому значению тока 3-й гармоники в нейтрали. В этом случае оказалось, что линейное напряжение, которое не содержит 3-й гармоники, меньше фазного, так как вследствие почти резонансного режима 3-я гармоника фазного напряжения больше основной.

Пример 12.13.

Найти показания приборов при тех же фазных ЭДС и сопротивлениях

Найти показания приборов при тех же фазных ЭДС и сопротивлениях, что и в примере 12.12, но при соединении фаз источника и приемника треугольником (рис. 12.22, б).

Решение. В этом случае 3-я гармоника замыкается в контуре генератора и .

Так как остальные составляющие те же, что и в примере 12.12, то

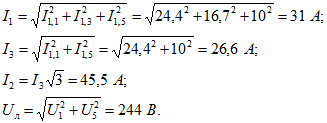
Таким образом, 3-я гармоника влияет только на внутренние токи источника и не сказывается на распределении токов и напряжений приемника.

Различные схемы соединения трехфазных цепей

Найти показания приборов при разомкнутом и замкнутом ключе

Найти показания приборов при тех же фазных ЭДС и сопротивлениях

Дополнительно по теме