Разложение периодической несинусоидальной кривой в тригонометрический ряд
Явления, происходящие в линейных цепях при периодических, но несинусоидальных ЭДС, напряжениях и токах, проще всего поддаются исследованию, если кривые ЭДС, напряжений и токов разложить в тригонометрические ряды Эйлера - Фурье.
Как известно, всякая периодическая функция ![]() , удовлетворяющая условиям Дирихле, т. е. имеющая на всяком конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд:
, удовлетворяющая условиям Дирихле, т. е. имеющая на всяком конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд:
![]()
Первый член ряда ![]() называется постоянной составляющей или нулевой гармоникой, второй член
называется постоянной составляющей или нулевой гармоникой, второй член ![]() - основной синусоидой или 1-й гармоникой, а все остальные члены вида
- основной синусоидой или 1-й гармоникой, а все остальные члены вида ![]() при k>1 носят название высших гармоник;
при k>1 носят название высших гармоник; ![]() - основная частота (угловая); Т - период несинусоидальной периодической функции.
- основная частота (угловая); Т - период несинусоидальной периодической функции.
Тригонометрический ряд после раскрытия синуса суммы для каждой из гармонических составляющих, или, короче, гармоник, записывается и в иной форме:
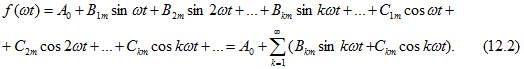
Здесь ![]() .
.
Коэффициенты ![]() могут быть вычислены при помощи следующих интегралов:
могут быть вычислены при помощи следующих интегралов:
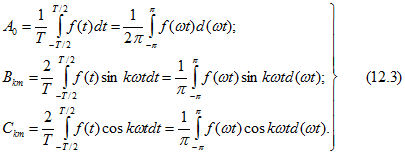
Постоянная составляющая ![]() равна среднему значению функции
равна среднему значению функции ![]() за ее период
за ее период ![]() .
.
Зная коэффициенты ряда (12.2), легко перейти к форме (12.1), подсчитывая
![]()
Вводя условно отрицательные частоты, т. е. переходя к суммированию по k от ![]() до
до ![]() , можно ряду (12.2) придать более компактный вид (где, по существу, каждая гармоника, кроме нулевой, входит под знак суммы дважды):
, можно ряду (12.2) придать более компактный вид (где, по существу, каждая гармоника, кроме нулевой, входит под знак суммы дважды):
![]()
Постоянная составляющая в этом выражении получается при k=0, что соответствует выражению (12.3), так как ![]() .
.
Выражению (12.2а) можно придать несколько иной вид, если воспользоваться формулами Эйлера для тригонометрических функций времени:
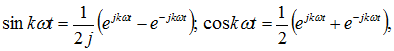
и вместо (12.2а) получим
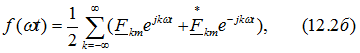
где согласно (12.3)
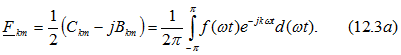
Учитывая, что ![]() а
а ![]() и что сумма двух комплексно-сопряженных величин равна их удвоенной действительной части, выражение (12.26) можно упростить. Оно принимает вид
и что сумма двух комплексно-сопряженных величин равна их удвоенной действительной части, выражение (12.26) можно упростить. Оно принимает вид
![]()
Комплексная форма ряда Фурье [(12.2в) и (12.3а)] имеет большое значение при переходе от дискретного спектра к непрерывному.
Рис. 12.4
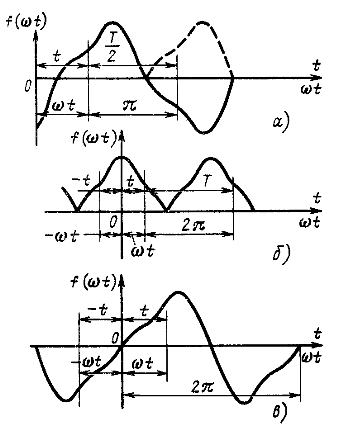
Значительное число непериодических функций времени, с которыми приходится встречаться в электротехнике (рис. 12.4, а), удовлетворяет условию
![]()
Функции, удовлетворяющие этому условию, называются симметричными относительно оси абсцисс. Они раскладываются в ряд, который не содержит четных гармоник и постоянной составляющей:
![]()
В схемах выпрямления переменного тока часто приходится встречаться с функциями, которые при соответствующем выборе начала координат удовлетворяют условию (рис. 12.4, 6)
![]()
Такие функции называются симметричными относительно оси ординат.
В этом случае ряд не содержит синусов:
![]()
В схемах умножения частоты встречаются функции, которые при выборе начала координат в точке нуля функции удовлетворяют условию (рис. 12.4, в)
![]()
Такие функции называются симметричными относительно начала координат и раскладываются в ряд, не содержащий косинусов и постоянной составляющей:
![]()
Примеры разложения в ряд некоторых простейших из наиболее часто встречающихся в электротехнике кривых приведены в приложении 3.
Если начало отсчета времени сдвигается, то соответственно изменяется вид ряда, в котором амплитуды гармоник остаются прежними, но изменяются их начальные фазы. Например, если перейти от функции ![]() , выражаемой рядом (12.1), к
, выражаемой рядом (12.1), к ![]() , т. е. сместить начало отсчета времени на
, т. е. сместить начало отсчета времени на ![]() , то получим ряд
, то получим ряд
![]()
где
![]()
Совокупность гармонических составляющих несинусоидальной периодической функции называется ее дискретным частотным спектром.
Спектр можно характеризовать некоторой зависимостью ![]() (спектр амплитуд) и (спектр фаз) от частоты
(спектр амплитуд) и (спектр фаз) от частоты ![]() .
.
Пример 12.1.
Построить спектр для несинусоидальной функции в виде ряда прямоугольных импульсов
Построить спектр для несинусоидальной функции в виде ряда прямоугольных импульсов продолжительностью ![]() с высотой
с высотой ![]() , следующих один за другим через интервалы времени
, следующих один за другим через интервалы времени ![]() (рис. 12.5, а). Напряжения такой формы встречаются в различных схемах телеграфии, телемеханики и автоматики.
(рис. 12.5, а). Напряжения такой формы встречаются в различных схемах телеграфии, телемеханики и автоматики.
Рис. 12.5
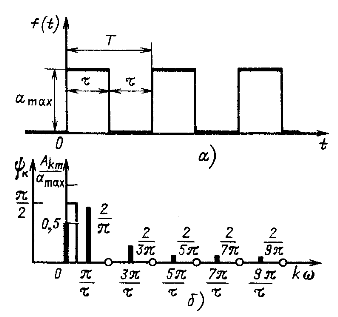
Решение. Найдя коэффициенты разложения по формулам (12.3) или выписав их из таблицы (приложение 3), представим рассматриваемую функцию в виде ряда
![]()
где ![]() .
.
Дискретный спектр амплитуд этих импульсов представлен на рис. 12.5, б. Там же показан спектр фаз, изображенный в виде непрерывной функции. Эта функция реально существует только в тех точках, где ![]() .
.
Пример 12.2.
Построить спектр той же функции, что в примере 12.1, при начале отсчета времени, сдвинутом на ![]() (рис. 12.6, а).
(рис. 12.6, а).
Рис. 12.6
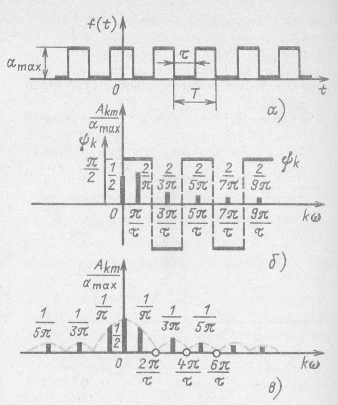
Решение. Эта функция симметрична относительно оси ординат, и ее разложение в тригонометрический ряд имеет вид:
![]()
Спектры амплитуд и фаз этой функции показаны на рис. 12.6, б. Естественно, что спектр амплитуд остался прежним.
Рассматривая каждую гармонику как сумму членов ряда для ![]() и переходя от записи (12.2) к (12.2а), можно этому выражению придать следующий вид:
и переходя от записи (12.2) к (12.2а), можно этому выражению придать следующий вид:
![]()
Действительно, при k=0
![]()
т. е. получаем постоянную составляющую; при четных значениях k члены ряда обращаются в нуль, а при k нечетных ![]() и при суммировании членов для положительных и отрицательных к дают амплитуду, равную
и при суммировании членов для положительных и отрицательных к дают амплитуду, равную ![]() .
.
Спектр амплитуд в этом случае имеет симметричный вид (рис. 12.6, в).
Такое рассмотрение гармонические составляющих как совокупности колебаний положительных и отрицательных часто во многих случаях позволяет получить более простое общее выражение. Отрицательная частота, конечно, не имеет физического смысла, и составляющие ряда при k<0 являются не чем иным, как удобным математическим выражением гармоник, имеющих положительную частоту, соответствующую модулю k.
Пример 12.3.
Построить спектр последовательности прямоугольных импульсов
Построить спектр последовательности прямоугольных импульсов продолжительностью ![]() с периодом повторения Т, причем
с периодом повторения Т, причем ![]() и
и ![]() может принимать любое значение в интервале
может принимать любое значение в интервале ![]() .
.
Решение. Выпишем из таблицы приложения 3 разложение этой функции в тригонометрический ряд:
![]()
где ![]()
Раскладывая каждую из гармоник на сумму двух синусоид, соответствующих положительным и отрицательным значениям k [см. (12.2а)], придадим выражению ![]() иную форму:
иную форму:
![]()
где постоянная составляющая получается при раскрытии неопределенности:
![]()
Обозначив ![]() , получим для
, получим для ![]() следующее выражение:
следующее выражение:
![]()
Рис. 12.7
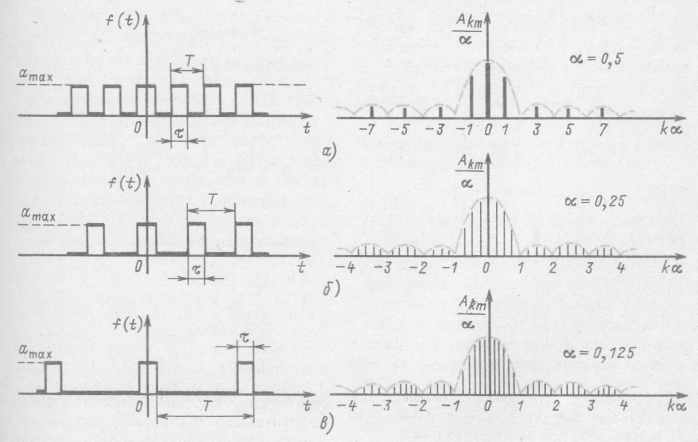
На рис. 12.7, а-в видно, что вне зависимости от периода повторения импульсов Т спектр имеет (с точностью до множителя a) одну и ту же зависимость амплитуд от частоты (огибающую). Чем больше период повторения импульсов, тем большее число гармонических составляющих укладывается на одном и том же участке огибающей и тем медленнее уменьшаются амплитуды гармонических составляющих с увеличением номера гармоники. Кроме того, чем больше период Т, тем меньше амплитуды гармонических составляющих.
Для исследования непериодических процессов большое значение имеет предельный переход при ![]() .
.
Пример 12.4.
Найти спектр последовательности очень коротких импульсов
Найти спектр последовательности очень коротких импульсов, длительность которых значительно меньше периода их повторения Т.
Изучение последовательности таких импульсов очень важно в различных задачах электротехники, в частности при рассмотрении импульсных и релейных систем автоматики.
Решение. Частотный спектр такой последовательности импульсов получается из выражения (12.12), приведенного в предыдущем примере, при ![]() :
:
![]()
Таким образом, спектр периодической последовательности кратковременных импульсов приближенно может быть выражен бесконечным множеством равных по амплитуде гармоник с частотами, кратными основной частоте импульсов ![]() . Амплитуда гармоник в
. Амплитуда гармоник в ![]() раз меньше, чем высота импульсов. Это соответствует среднему участку спектра, представленного на рис. 12.7, при стремлении периода огибающей, которая изображена на этом рисунке штриховой линией, к бесконечности (при
раз меньше, чем высота импульсов. Это соответствует среднему участку спектра, представленного на рис. 12.7, при стремлении периода огибающей, которая изображена на этом рисунке штриховой линией, к бесконечности (при ![]() ), если, конечно, по оси абсцисс откладывать не
), если, конечно, по оси абсцисс откладывать не ![]() , а просто k или
, а просто k или ![]() .
.
Дополнительно по теме
- Периодические несинусоидальные токи и напряжения в электрических цепях
- Несинусоидальные ЭДС, напряжения и токи
- Максимальные, действующие и средние значения несинусоидальных периодических ЭДС, напряжений и токов
- Коэффициенты, характеризующие форму несинусоидальных периодических кривых
- Несинусоидальные кривые с периодической огибающей
- Действующие значения ЭДС, напряжений и токов с периодическими огибающими
- Расчет цепей с несинусоидальными периодическими ЭДС, напряжениями и токами
- Резонанс в цепи несинусоидального тока
- Мощность в цепи несинусоидального тока
- Высшие гармоники в трехфазных цепях

