Расчет магнитной цепи с постоянным магнитом
На рис. 24.12 схематически показан стальной магнитопровод в виде кольца с воздушным зазором. Определим магнитный поток в воздушном зазоре, если магнитопровод предварительно намагничен до насыщения. Размеры магнитопровода и кривая размагничивания В(Н) для материала заданы.
Если в магнитопроводе нет воздушного зазора, что соответствует введению в воздушный зазор пластины из магнитного материала с очень большим значением ![]() , то после намагничивания магнитная индукция в магнитопроводе равна остаточной индукции
, то после намагничивания магнитная индукция в магнитопроводе равна остаточной индукции ![]() , а напряженность магнитного поля равняется нулю. Это непосредственно следует из закона полного тока
, а напряженность магнитного поля равняется нулю. Это непосредственно следует из закона полного тока ![]() , поскольку намагничивающий ток отсутствует. На петле гистерезиса такое состояние соответствует верхней точке кривой размагничивания (см. рис. 24.1 и 24.5).
, поскольку намагничивающий ток отсутствует. На петле гистерезиса такое состояние соответствует верхней точке кривой размагничивания (см. рис. 24.1 и 24.5).
При наличии воздушного зазора напряженность поля не равна нулю, что легко показать, пользуясь законом полного тока. Магнитная цепь в этом случае состоит из двух участков: стального магнитопровода, в котором напряженность поля ![]() можно считать одинаковой во всех точках средней линии, и воздушного зазора, напряженность магнитного поля в котором связана с магнитной индукцией известной зависимостью
можно считать одинаковой во всех точках средней линии, и воздушного зазора, напряженность магнитного поля в котором связана с магнитной индукцией известной зависимостью ![]() .
.
При незначительной длине воздушного зазора можно принять сечение воздушного зазора ![]() равным сечению магнитопровода
равным сечению магнитопровода ![]() , т. е. считать индукцию во всех точках магнитной цепи одинаковой:
, т. е. считать индукцию во всех точках магнитной цепи одинаковой:
![]()
Выбирая путь интегрирования вдоль средней линии по направлению вектора магнитной индукции ![]() , напишем следующее выражение:
, напишем следующее выражение:
![]()
откуда
![]()
где ![]() называется коэффициентом размагничивания по индукции.
называется коэффициентом размагничивания по индукции.
Следовательно, в этом случае несмотря на отсутствие намагничивающих токов напряженность магнитного поля во всех точках кольцевого магнитопровода не равна нулю. В воздушном промежутке направление вектора напряженности поля совпадает с направлением вектора магнитной индукции, а внутри магнитопровода, как следует из (24.14), они направлены противоположно (рис. 24.12).
Рис. 24.12
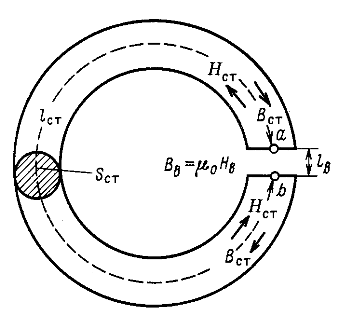
Отрицательное значение напряженности магнитного поля внутри сердечника означает, что при наличии воздушного зазора магнитная индукция ![]() меньше остаточной индукции
меньше остаточной индукции ![]() , т. е.
, т. е. ![]() при Н < 0.
при Н < 0.
Так как отрицательному значению напряженности магнитного поля ![]() соответствуют положительные значения индукции
соответствуют положительные значения индукции ![]() , то магнитное состояние магнитопровода определяется одной из точек кривой размагничивания (второй квадрант петли гистерезиса).
, то магнитное состояние магнитопровода определяется одной из точек кривой размагничивания (второй квадрант петли гистерезиса).
Для расчета рассматриваемой магнитной цепи построим зависимость магнитного потока ![]() от магнитного напряжения
от магнитного напряжения ![]() , взятого в направлении вектора
, взятого в направлении вектора ![]() между точками а и b концов магнитопровода; эта зависимость получается из кривой размагничивания путем простого умножения ее ординат на
между точками а и b концов магнитопровода; эта зависимость получается из кривой размагничивания путем простого умножения ее ординат на ![]() и абсцисс - на
и абсцисс - на ![]() (рис. 24.13). На том же рисунке построим зависимость магнитного потока воздуха
(рис. 24.13). На том же рисунке построим зависимость магнитного потока воздуха ![]() от магнитного напряжения, взятого в направлении
от магнитного напряжения, взятого в направлении ![]() между теми же точками а и b магнитопровода. Это напряжение
между теми же точками а и b магнитопровода. Это напряжение
![]()
откуда
![]()
Из последнего выражения следует, что магнитный поток ![]() пропорционален магнитному напряжению
пропорционален магнитному напряжению ![]() (прямая линия на рис. 24.13). Отметим, что магнитное сопротивление воздушного зазора в действительности несколько меньше определяемого по формуле
(прямая линия на рис. 24.13). Отметим, что магнитное сопротивление воздушного зазора в действительности несколько меньше определяемого по формуле ![]() , так как магнитный поток в воздушном зазоре распределяется по большей площади, чем поперечное сечение магнитопровода (
, так как магнитный поток в воздушном зазоре распределяется по большей площади, чем поперечное сечение магнитопровода (![]() ).
).
Так как магнитный поток в магнитопроводе равен потоку в воздушном зазоре, т. е. ![]() , и магнитное напряжение
, и магнитное напряжение ![]() , то магнитный поток определится ординатой точки
, то магнитный поток определится ординатой точки ![]() пересечения кривой
пересечения кривой ![]() и прямой
и прямой ![]() (рис. 24.13).
(рис. 24.13).
Опустив из точки ![]() перпендикуляр
перпендикуляр ![]() на ось абсцисс, получим отрезок Оm, определяющий магнитное напряжение между точками а и b.
на ось абсцисс, получим отрезок Оm, определяющий магнитное напряжение между точками а и b.
Определим теперь магнитный поток в воздушном зазоре в том случае, если после намагничивания стального магнитопровода длина воздушного зазора будет уменьшена введением ферромагнитного диска с площадью ![]() . Магнитную проницаемость материала диска будем считать такой высокой, что магнитным сопротивлением диска можно пренебречь.
. Магнитную проницаемость материала диска будем считать такой высокой, что магнитным сопротивлением диска можно пренебречь.
Рис. 24.13
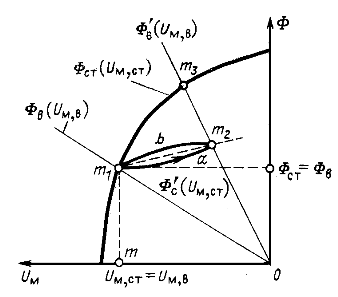
В этом случае длина зазора станет меньше, а значит, уменьшится его магнитное сопротивление до величины ![]() . Зависимость магнитного потока в воздушном зазоре от напряжения
. Зависимость магнитного потока в воздушном зазоре от напряжения ![]() представится прямой
представится прямой ![]() с большим углом наклона к оси абсцисс, чем у прямой
с большим углом наклона к оси абсцисс, чем у прямой ![]() (рис. 24.13). Но поток в стальном магнитопроводе будет расти не по кривой размагничивания
(рис. 24.13). Но поток в стальном магнитопроводе будет расти не по кривой размагничивания ![]() , а по кривой
, а по кривой ![]() частного цикла, т. е.
частного цикла, т. е. ![]() , которую можно заменить приближенно прямой линией. Точка пересечения
, которую можно заменить приближенно прямой линией. Точка пересечения ![]() с прямой
с прямой ![]() и определяет искомое значение потока в воздушном зазоре
и определяет искомое значение потока в воздушном зазоре ![]() .
.
Если магнитопровод намагнитить при вставленном стальном диске, то магнитный поток будет значительно больше и определится ординатой точки ![]() . При удалении диска из воздушного зазора магнитопровод будет размагничиваться и поток уменьшится до значения, определяемого ординатой точки
. При удалении диска из воздушного зазора магнитопровод будет размагничиваться и поток уменьшится до значения, определяемого ординатой точки ![]() . При введении стального диска в зазор магнитный поток возрастет только до значения, определяемого ординатой точки
. При введении стального диска в зазор магнитный поток возрастет только до значения, определяемого ординатой точки ![]() .
.
Из графического построения, приведенного на рис. 24.13, видно влияние параметров магнитной цепи на значение магнитного потока. В частности, увеличение длины магнита и применение материала с большей коэрцитивной силой ![]() приводит к относительному увеличению абсцисс кривой
приводит к относительному увеличению абсцисс кривой ![]() , а увеличение сечения магнита
, а увеличение сечения магнита ![]() и применение материала с большей остаточной индукцией
и применение материала с большей остаточной индукцией ![]() при той же коэрцитивной силе приводит к увеличению ординат кривой
при той же коэрцитивной силе приводит к увеличению ординат кривой ![]() . И увеличение абсцисс, и увеличение ординат приводит к возрастанию магнитного потока Ф.
. И увеличение абсцисс, и увеличение ординат приводит к возрастанию магнитного потока Ф.
Пример 24.4.
Определить магнитную индукцию в воздушном зазоре гальванометра
Определить магнитную индукцию в воздушном зазоре гальванометра в двух случаях:
1. Магнитная цепь подковообразного магнита (рис. 24.14), состоящая из постоянного магнита 1, полюсных наконечников 2 и сердечника 3, была намагничена до насыщения в собранном виде.
2. Намагничивание до насыщения производилось при вынутом цилиндрическом сердечнике, и сердечник был вставлен после намагничивания.
Магнитным рассеянием, а также магнитным сопротивлением сердечника и полюсных наконечников пренебречь. В первом случае расчетные размеры: длина средней линии магнита ![]() ; сечение магнита
; сечение магнита ![]() ; длина воздушного зазора
; длина воздушного зазора ![]() ; сечение воздушного зазора
; сечение воздушного зазора ![]() . При вынутом сердечнике
. При вынутом сердечнике ![]() . Кривая размагничивания магнита (спинка) характеризуется следующими данными
. Кривая размагничивания магнита (спинка) характеризуется следующими данными
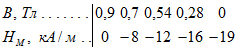
Кривую возврата считать прямой с наклоном ![]() .
.
Решение. Строим зависимость ![]() , где
, где ![]()
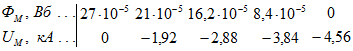
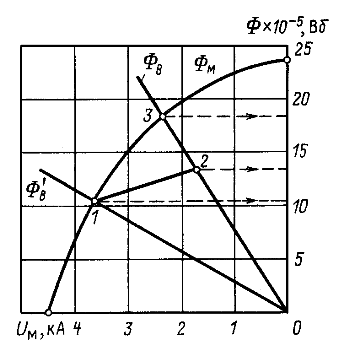
Строим зависимость ![]() (рис. 24.15).
(рис. 24.15).
При вставленном сердечнике
![]()
При вынутом сердечнике
![]()
Прямые ![]() и
и ![]() на рис. 24.15 соответственно 0 - 3 и 0 - 1.
на рис. 24.15 соответственно 0 - 3 и 0 - 1.
Из графика находим при вставленном сердечнике ![]() (точка 3). Индукции
(точка 3). Индукции
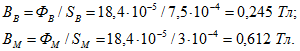
При вынутом сердечнике ![]() (точка 1).
(точка 1).
Наклон кривой возврата
![]()
При вынутом и вновь вставленном сердечнике (точка 2 на кривой возврата) находим:
![]()
По сравнению с индукцией в зазоре при намагничивании в собранном виде индукция уменьшилась на ![]()
Рис. 24.14
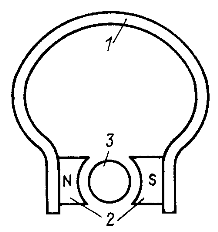
Рис. 24.15
Дополнительно по теме
- Основные величины, характеризующие магнитное поле
- Основные понятия и законы магнитных цепей
- Ферромагнитные материалы и их характеристики
- Анализ и синтез неразветвленных магнитных цепей
- Примеры магнитных цепей электрических машин
- Расчет разветвленных магнитных цепей

