Расчет цепи с несимметричной нагрузкой
В нормальных условиях несимметричные режимы в высоковольтных трехфазных цепях встречаются относительно редко (преимущественно в цепях с дуговыми электроплавильными печами и однофазными электротяговыми двигателями). Обычно несимметричные режимы получаются в аварийных условиях, когда в какой-либо цепи появляется несимметрия.
Различают два вида несимметрии - поперечную и продольную. Поперечная несимметрия у симметричной трехфазной цепи возникает при несимметричной нагрузке. К ней, в частности, относятся различные виды несимметричных коротких замыканий (замыкания между фазами, замыкание одной или двух фаз на землю). Продольная несимметрия возникает, если в рассечку фаз линии включаются элементы с неодинаковыми сопротивлениями или при обрыве одного или двух проводов (несимметричный участок линии).
Для расчетов несимметричных режимов трехфазных цепей удобно пользоваться принципом компенсации, заменяя несимметричный приемник или несимметричный участок в линии источниками ЭДС (напряжений), значения которых до окончания всего расчета остаются неизвестными. Целесообразность этого приема заключается в том, что после такой замены цепь становится симметричной и для нее разноименные симметричные составляющие токов и напряжений не зависят друг от друга. Связи же между симметричными составляющими токов и напряжений различных последовательностей, обусловленные несимметрией, вводятся позднее.
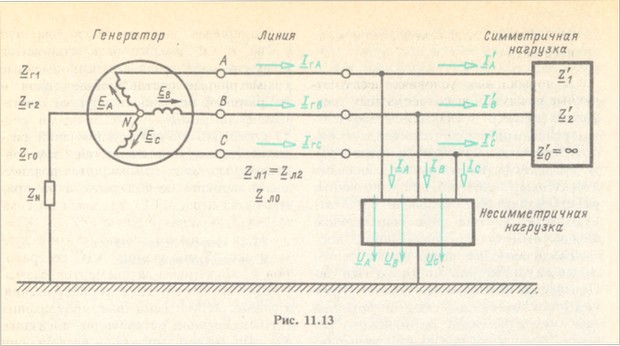
Рассмотрим метод расчета на примере схемы рис. 11.13, содержащей симметричную динамическую (![]() ) и несимметричную статическую нагрузки. Пусть заданы ЭДС генераторов и сопротивления элементов схемы. Требуется найти токи и напряжения. На рис. 11.13 схема и сопротивления несимметричной нагрузки не показаны, так как на первом этапе расчета они не нужны.
) и несимметричную статическую нагрузки. Пусть заданы ЭДС генераторов и сопротивления элементов схемы. Требуется найти токи и напряжения. На рис. 11.13 схема и сопротивления несимметричной нагрузки не показаны, так как на первом этапе расчета они не нужны.
Заменим несимметричную нагрузку тремя источниками ЭДС с неизвестными напряжениями ![]() и получим симметричную схему, которая помимо генератора с симметричной системой ЭДС содержит источники с несимметричными напряжениями
и получим симметричную схему, которая помимо генератора с симметричной системой ЭДС содержит источники с несимметричными напряжениями ![]() .
.
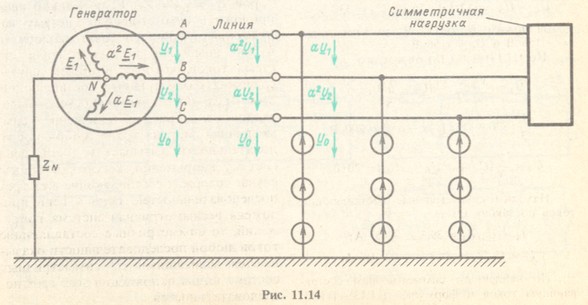
Разложим напряжения ![]() на симметричные составляющие
на симметричные составляющие ![]() , приняв фазу А за основную. В результате получим симметричную схему (рис. 11.14), причем в ответвлении, где была несимметричная нагрузка, находятся источники трех симметричных систем напряжений прямой, обратной и нулевой последовательностей.
, приняв фазу А за основную. В результате получим симметричную схему (рис. 11.14), причем в ответвлении, где была несимметричная нагрузка, находятся источники трех симметричных систем напряжений прямой, обратной и нулевой последовательностей.
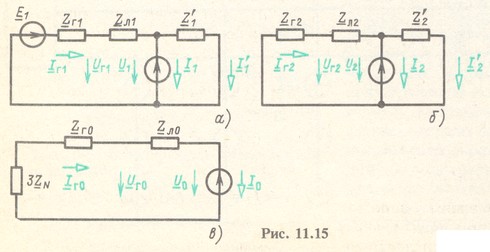 В симметричной цепи симметричная система напряжений какой-либо последовательности вызывает симметричную систему токов той же самой последовательности. Следовательно, можно составить три независимые схемы, показанные на рис. 11.15, а-в. Для упрощения в этих схемах не учтены частичные емкости линии (см. раздел).
В симметричной цепи симметричная система напряжений какой-либо последовательности вызывает симметричную систему токов той же самой последовательности. Следовательно, можно составить три независимые схемы, показанные на рис. 11.15, а-в. Для упрощения в этих схемах не учтены частичные емкости линии (см. раздел).
Режим фазы А исходной схемы (см. рис. 11.13) определим путем наложения режимов этих трех схем.
Конфигурации схем прямой и обратной последовательностей всегда одинаковы. Схема нулевой последовательности обычно существенно отличается. В данном примере она не имеет разветвления, так как в правой части трехфазной цепи (см. рис. 11.13) токов нулевой последовательности не может быть. Следует обратить особое внимание на то, что сопротивление в нейтральном проводе вводится в схему нулевой последовательности утроенной величиной (см. раздел).
Из рассмотрения составленных схем видно, что наибольшие значения симметричных составляющих напряжений обратной и нулевой последовательностей наблюдаются в месте подключения несимметричного приемника, так как в схемах именно там находятся источники ЭДС обратной и нулевой последовательностей.
Для дальнейшего расчета целесообразно преобразовать схемы отдельных последовательностей к простейшему виду, не затрагивая при этом ветвей с источниками неизвестных напряжений ![]() .
.
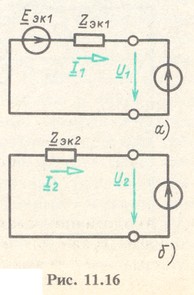 В схеме прямой последовательности заменим ветви генератора и симметричного приемника эквивалентным генератором (рис. 11.16, а):
В схеме прямой последовательности заменим ветви генератора и симметричного приемника эквивалентным генератором (рис. 11.16, а):
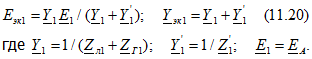
В схеме обратной последовательности объединяем ветви генератора и симметричного приемника (рис. 11.16,б):
![]()
Схема нулевой последовательности в данном примере в преобразовании не нуждается, так как она имеет простейший вид.
Для каждой из трех схем напишем уравнения по второму закону Кирхгофа:
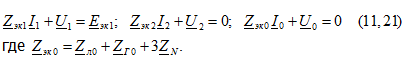
В этих трех уравнениях шесть неизвестных: ![]() Дополнительные три уравнения, связывающие эти шесть неизвестных величин, могут быть составлены на основании заданной схемы и параметров несимметричного приемника.
Дополнительные три уравнения, связывающие эти шесть неизвестных величин, могут быть составлены на основании заданной схемы и параметров несимметричного приемника.
Рис. 11.16
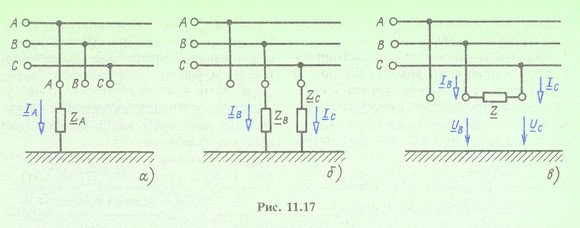
Составим дополнительные уравнения для некоторых видов несимметричных приемников. Для приемника, представленного на рис. 11.17, а
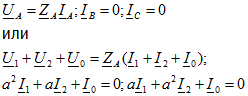
Для приемника, показанного на рис. 11.17,6
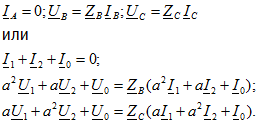
При отсутствии соединения несим-метричного приемника с землей, например, для схемы, приведенной на рис. 11.17, в,симметричные составляющие токов нулевой последовательности равны нулю и составление схемы цепи нулевой последовательности на предыдущих этапах расчета выпадает. Получаются два основных уравнения с четырьмя неизвестными, и нужно составить только два дополнительных уравнения, а именно:
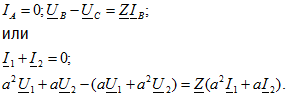
Аналогично составляют дополнительные уравнения и при других видах статической несимметричной нагрузки. При совместном решении уравнений Кирхгофа для схем различных последовательностей с дополнительными уравнениями определяются симметричные составляющие тока фазы А в ответвлении к несимметричному приемнику. Затем находят распределение этих составляющих по отдельным ветвям схем прямой, обратной и нулевой последовательностей. Зная составляющие токов в любой ветви, вычисляют действительный ток в каждой фазе и составляющие падений напряжения различных последовательностей, а затем и фазные напряжения на отдельных участках схемы.
Приведем расчет режима схемы (см. рис. 11.13) для случая несимметричной нагрузки, представленной на рис. 11.17, a при условии, что ![]() (однофазное замыкание на землю). Составим дополнительные уравнения
(однофазное замыкание на землю). Составим дополнительные уравнения
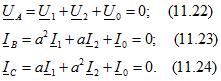
Вычитая (11.24) из (11.23), получаем
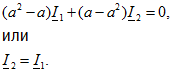
Подставляя этот результат в (11.23), имеем
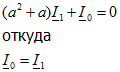
Заменяем в (11.21) ![]() затем их суммируем и с учетом (11.22) получим
затем их суммируем и с учетом (11.22) получим
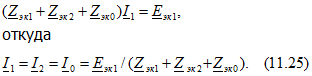
Симметричные составляющие напряжений (в месте замыкания на землю) определяются из (11.21):
![]()
Для схем рис. 11.15, а
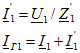
рис. 11.15, б
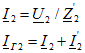
рис. 1115, в
![]()
Симметричные составляющие напряжений на выводах генератора могут быть найдены по тем же схемам на рис. 11.15:
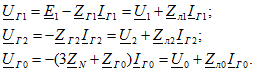
Дополнительно по теме
- Симметричные составляющие трехфазной системы
- Свойства трехфазных цепей в отношении симметричных составляющих
- Сопротивления симметричной трехфазной цепи для токов различных последовательностей
- Определение токов в симметричной цепи
- Симметричные составляющие напряжений и токов в несимметричной трехфазной цепи
- Расчет цепи с несимметричным участком в линии
- Нелинейные цепи

