Свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений

В нейтральном проводе ток равен сумме линейных токов и, следовательно, тройному значению составляющей тока нулевой последовательности [см. (11.16)].

Сумма линейных напряжений равна нулю, поэтому линейные напряжения не содержат составляющих нулевой последовательности.

Симметричные составляющие прямой и обратной последовательностей фазных напряжений приемника, соединенного звездой, однозначно связаны с соответствующими симметричными составляющими подведенных к нему линейных напряжений. Отсюда следует, что фазные напряжения различных приемников, соединенных звездой, при одних и тех же линейных напряжениях имеют одинаковые симметричные составляющие прямой и обратной последовательностей и могут отличаться друг от друга только за счет симметричных составляющих нулевой последовательности.

Если при несимметричном режиме ток в одной или двух фазах цепи отсутствует, сумма симметричных составляющих токов в этих фазах равна нулю. Поясним сказанное примерами.

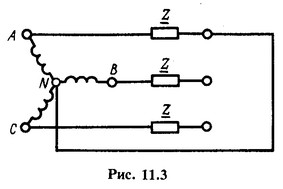
В схеме, показанной на рис. 11.3, фазы В и С разомкнуты, . Применяя (11.16) -(11.18), получаем

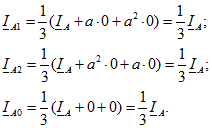
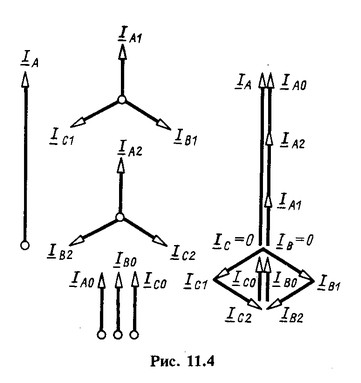
На рис. 11.4 изображен вектор тока и построены векторные диаграммы для систем симметричных составляющих токов всех трех фаз. Там же проведено геометрическое суммирование векторов симметричных составляющих токов, показывающее, что

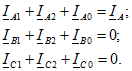
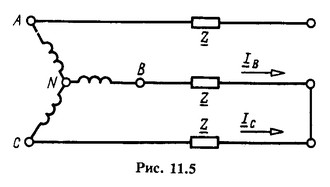
В схеме рис. 11.5 токи . По формулам (11.16) - (11.18) получим

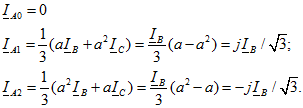
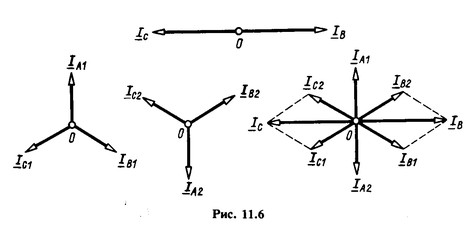
На рис. 11.6 показаны векторная диаграмма токов и векторные диаграммы симметричных составляющих токов всех трех фаз. Геометрическое суммирование векторов показывает, что

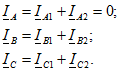
Симметричные составляющие токов и напряжений могут быть не только вычислены, но и измерены при помощи специальных электрических измерительных схем, называемых фильтрами симметричных составляющих токов и напряжений. Эти фильтры получили широкое применение в релейной защите электроэнергетических цепей.

Дополнительно по теме