Сведение расчета переходного процесса к нулевым начальным условиям

При изучении переходных процессов в электрических машинах, в схемах автоматического регулирования и в других случаях часто сводят их расчет при ненулевых начальных условиях к расчету при нулевых начальных условиях следующим приемом.

Рис. 15.6

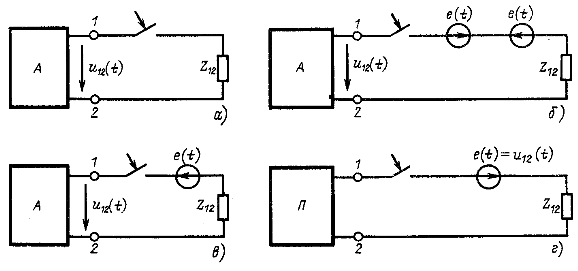
Пусть к выводам 1-2 активного двухполюсника ключом Р подключается ветвь с операторным сопротивлением (рис. 15.6, а). Если в подключаемой ветви есть источники ЭДС и тока или заряженные конденсаторы, то отнесем их в состав активного двухполюсника.

Для расчета тока в подключаемой ветви (в ветви ключа) или в какой-либо иной ветви активного двухполюсника определим прежде всего напряжение на выводах 1-2 ключа до его включения, обусловленное всеми источниками активного двухполюсника. В ветвь ключа включим (рис. 15.6,6) два источника с противоположно направленными ЭДС . При этом режим в цепи не изменится.

Теперь рассмотрим включение ключа. Так как система линейна, будем вести расчет методом наложения. Прежде всего найдем токи при действии всех источников активного двухполюсника и той ЭДС, которая действует противоположно напряжению (рис. 15.6, в). В этой схеме включается ветвь с источником ЭДС e(t), равной и противоположной по направлению эквивалентной ЭДС активного двухполюсника. Поэтому в этой схеме ток в ветви ключа после его замыкания остается равным нулю, а значит, для всей схемы в целом это будет режим до коммутации. Остается учесть последнюю ЭДС e(t), действующую в ветви ключа в том же направлении, что и напряжение (рис. 15.6, г), т.е. рассчитать переходный процесс при включении ветви с источником ЭДС e(t) к пассивному двухполюснику или, иначе говоря, при нулевых начальных условиях.

Если при включении рубильника определяется ток в какой-нибудь ветви активного двухполюсника, то нужно в соответствии со сказанным учесть, что он состоит из тока, существовавшего в этой ветви до коммутации, и тока, который возникает в этой ветви после включения источника ЭДС е(t) к пассивному двухполюснику (рис. 15.6, г). Если, в частности, рассчитывается ток в ветви ключа (равный нулю до коммутации), достаточно рассчитать режим в схеме на рис. 15.6, г.

Свести расчет переходных процессов в цепи с ненулевыми начальными условиями к расчету при нулевых начальных условиях можно, применяя как классический, так и операторный метод. Сопротивление может быть в общем случае входным сопротивлением другого пассивного двухполюсника, подключаемого к выводам 1-2.

Аналогично можно показать, что отключение любой ветви, не содержащей индуктивного элемента, можно свести к включению в нее источника тока с током, равным и противоположным по направлению току в этой ветви до коммутации.

Пример 15.4.

Рис. 15.7

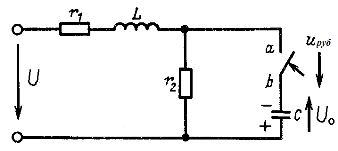
Найти ток в конденсаторе (рис. 15.7) после включения ключа, если .

Решение. Будем считать активным двухполюсником всю схему, кроме ключа, т. е. согласно рис. 15.6 . Выбрав положительное направление напряжения на ключе, как указано на рис. 15.7, найдем это напряжение:

Входное сопротивление активного и соответствующего пассивного двухполюсника (рис. 15.6, г)

Изображение искомого тока найдем по закону Ома в операторной форме (15.19):

Приравнивая нулю, находим корни характеристического уравнения: . Оригинал (ток i) найдем по теореме разложения (15.10). В соответствии с замечаниями, сделанными о применении теоремы разложения при комплексных корнях,

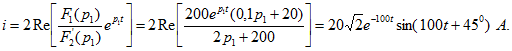
Дополнительно по теме