Математическое описание переходных процессов

Дополнительно по теме

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ СИСТЕМАХ

Основные сведения

При классификации переходных процессов, различают волновые процессы, электромагнитные и электромеханические. Здесь рассмотрены два последних вида переходных процессов.

Из общих уравнений Парка - Горева, изложенных ниже, могут быть найдены значения токов при любых переходных процессах в системах, в том числе при коротких замыканиях, однако в этом разделе не приводятся расчетные выражения для определения этих токов.

Расчеты по уравнениям Парка - Горева (П.-Г.) довольно сложны и проводятся только при применении вычислительных машин. Обычно при аналитических расчетах, расчетах с помощью статических моделей (расчетных столов) и значительной части расчетов, выполняемых на вычислительных машинах, целесообразно пользоваться упрощенными уравнениями. Правильный выбор системы уравнений и необходимой точности анализа, соответствующей реальной технической задаче, составляет искусство инженера.

Дифференциальные уравнения синхронных машин дают возможность проводить анализ переходных процессов в электрических системах с учетом наибольшего количества влияющих факторов (изменений угловой скорости ротора, апериодических составляющих токов статора, периодических токов ротора, активного сопротивления в цепи статора генератора). Опустив те или иные члены в уравнениях П. - Г., можно получить упрощенные уравнения, применяющиеся: а) для расчетов токов коротких замыканий (без учета изменений скорости); б) для расчета электромеханических переходных процессов, обычно без учета апериодических составляющих тока, статора и периодических тока ротора.

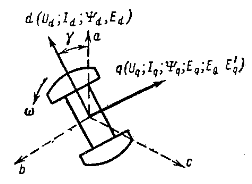
Уравнения П. - Г. связывают мгновенные значения токов, магнитных потоков, напряжений в осях координат (d, q), жестко связанных с ротором.

Мгновенные значения параметров режима - фазные и в осях d, q

Эти значения определяют как проекции на оси времени фаз а, b, с вектора тока, вращающегося со скоростью w. Этот вектор тока (напряжения, э. д. с, потокосцепления) называют обобщенным.

Оси времени фаз, а, b, с неподвижны и совпадают с осями обмоток статора (рис. 37-1):

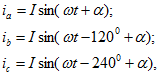
где a - произвольный угол.

Проекции обобщенного вектора тока на оси d и q, жестко связанные с ротором, дают значения, продольного и поперечного токов (рис. 37-2):

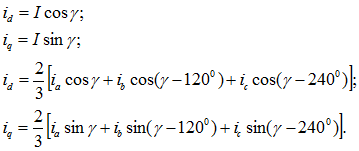
При наличии токов нулевой последовательности в системе имеет место соотношение

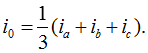
Соотношения, аналогичные приведенным выше, справедливы для напряжений, э. д. с. и потокосцеплений.

Соотношения между мгновенными значениями фазных величин и величинами в продольной и поперечной осях имеют вид:

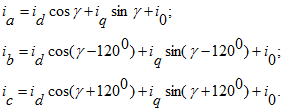
Угол g меняется во времени:

где - полное потокосцепление статора в продольной оси; - то же в поперечной оси; - ток нулевой последовательности.

В случае симметричного режима системы токи нулевой последовательности отсутствуют и выражения упрощаются.

Значения и определяются из выражений:

где G(p)-операторная проводимость машины; Xd(p)-операторное сопротивление машины в продольной оси; Xq(p)-то же в поперечной оси; Uв - напряжения возбуждения машины.

Для машины без успокоительных обмоток и эквивалентных им контуров

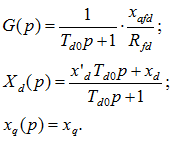
Если известна э. д. с. Eq, по можно найти так:

Для машины с успокоительными обмотками в продольной и поперечной осях и определяются теми же уравнениями.

Рис.37-1

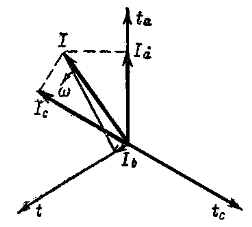
Рис. 37-2. Положение обобщенного вектора тока I в пространстве и его проекции на продольную и поперечную оси ротора.

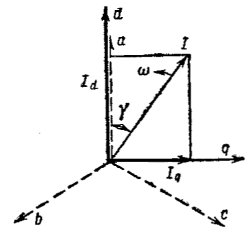
Уравнения Парка - Горева для синхронной машины в операторной форме

Эти уравнения при принятых на рис. 37-3 направлениях осей имеют вид:

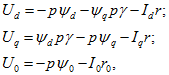
где

В системе относительных единиц ; тогда .

Рис. 37-3

Третье уравнение системы относится к случаю несимметричного режима или несимметричной схемы.

Уравнения, приведенные выше, полностью описывают переходный процесс машины, работающей на шины неизменного напряжения. Для анализа переходного процесса в сложной системе уравнения составляются для каждого элемента (генераторов, нагрузок, участков сети) и решаются совместно.

Решение уравнений, описывающих переходный процесс в системе

Решение приведенной выше системы уравнений относительно токов или других величин, рассматриваемых как неизвестные, проводится в операторной форме (для изображений). Например, находятся значения токов в виде:

где D1(p), D2(p)-частные определители системы; D(p)-общий определитель системы.

Характер переходного процесса в системе определяется знаком вещественной части корней определителя D(p). При переходный процесс затухающий.

Если изменения напряжений заданы, то можно записать:

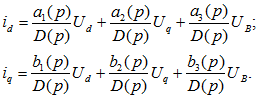
Токи как функции времени находят, переходя от изображения к оригиналам, что может быть сделано с помощью формулы разложения.

Уравнения для вращающего момента и мощности во время относительного движения ротора

При принятых направлениях осей (рис. 37-3) момент электромагнитных сил, действующих на ротор, в общем случае имеет вид

При подстановке и выраженных через токи и реактивные сопротивления, электромагнитный момент может быть вычислен согласно

В системе относительных единиц, где коэффициент 3/2 учтен соответствующим выбором базисных величин,

Связь между мощностью, отдаваемой в сеть, и моментом следующая:

где в относительных единицах;

Электромагнитная мощность генератора, передаваемая с ротора на статор,

Уравнение относительного движения ротора в общем виде:

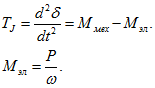
В относительных единицах

Упрощенные уравнения Парка - Горева для определения параметров режима при переходных электромеханических процессах

Эти уравнения применяются при расчетах токов коротких замыканий, устойчивости и т. д. При этом отказываются от учета влияния:

1) апериодической составляющей тока статора (трансформаторной э. д. с);

2) периодических токов ротора, связанных с апериодическими составляющими тока статора;

3) активного сопротивления в цепи статора.

Тогда в системе относительных единиц при уравнения П.- Г. для синхронной машины будут иметь вид:

В соответствии с этим упрощаются выражения для токов:

Выражения мощности и электромагнитного момента в этих условиях будут совпадать, так как при принятых предпосылках отдаваемая мощность численно равна вращающему моменту. Для симметричного или условно приведенного к симметричному режима (метод симметричных составляющих) получим:

Здесь и берутся с учетом принятых допущений.

Уравнение относительного движения ротора при принятых допущениях имеет вид

На основе упрощенного выражения момента можно перейти к ряду частных его выражений.

Дополнительно по теме

Математическое описание переходных процессов в электрических системах

Переходные процессы при больших кратковременных возмущениях и малых изменениях скорости

Режимы при больших возмущениях и больших изменениях скорости

Режимы при малых возмущениях и малых изменениях скорости

Меры улучшения устойчивости и пропускной способности электрических систем и электропередач