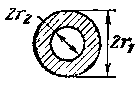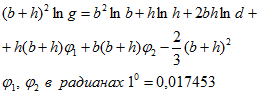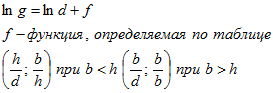Определение активного и реактивного сопротивлений шинопровода
Определение активного и реактивного сопротивлений шинопровода
ОПРЕДЕЛЕНИЕ АКТИВНОГО И РЕАКТИВНОГО СОПРОТИВЛЕНИЙ ШИНОПРОВОДА
а) Активное сопротивление шинопровода
При определении активного сопротивления за основу принимается омическое сопротивление, которое вычисляют по формуле
где 
— удельное сопротивление проводника, 
, при температуре 
(обычно 
принимают равным 20°С); l — длина проводника, м; s — сечение проводника, 
; 
— температурный коэффициент изменения сопротивления (для меди и алюминия 
); 
— температура, при которой определяется сопротивление проводника, °С
Как изложено в разделе, активное сопротивление проводника увеличивается за счет поверхностного эффекта, эффекта близости и потерь на гистерезис и вихревые токи в металлических конструкциях или стальной арматуре железобетонных конструкций шинопроводов.
Увеличение сопротивления проводника за счет поверхностного эффекта и эффекта близости учитывается введением коэффициента дополнительных потерь из ( 10-4), а именно:
Увеличение активного сопротивления шинопровода за счет потерь в металлических конструкциях, заключающих в себе шинопровод, учитывается введением в расчеты коэффициента 
:
Полное активное сопротивление шинопровода, Ом, определяется выражением
или в удельных величинах (Ом/км)
б) Реактивное сопротивление шинопровода
Для шинопроводов большой протяженности (длина значительно превышает линейные размеры шинопровода в поперечном разрезе) индуктивность шинопровода, Гн/км, подсчитывают по формуле
где l — длина шинопровода, см; g — среднегеометрическое расстояние площади поперечного сечения пакета шин от самого себя, см.
Взаимную индуктивность, Гн/км, для этого же случая определяют по формул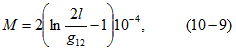е
где 
— среднегеометрическое расстояние между двумя пакетами шинопровода, см.
Пакет шин, состоящий из нескольких полос, должен рассматриваться как один проводник, но с соответствующим для его исполнения среднегеометрическим расстоянием. Среднегеометрические расстояния площадей сечения друг от друга и самих от себя могут быть наедены из табл. 10-1.
Таблица 10-1 Формулы для определения среднегеометрического расстояния шин в зависимости от конструктивного исполнения шинопровода
Фигура и обозначение размеров на ней |
Формула для определения среднегеометрического расстояния фигуры самой от себя |
Параметры фигуры |
|
|
Площадь круга |
|
|
Площадь кольца |
|
|
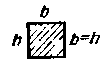
Площадь прямоугольника |
|
|
Периметр прямоугольника |
|
|
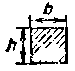
Периметр квадрата |
|
|
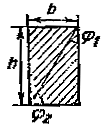
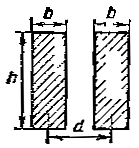
Между площадями двух одинаковых прямоугольников |
Таблица определения функции f
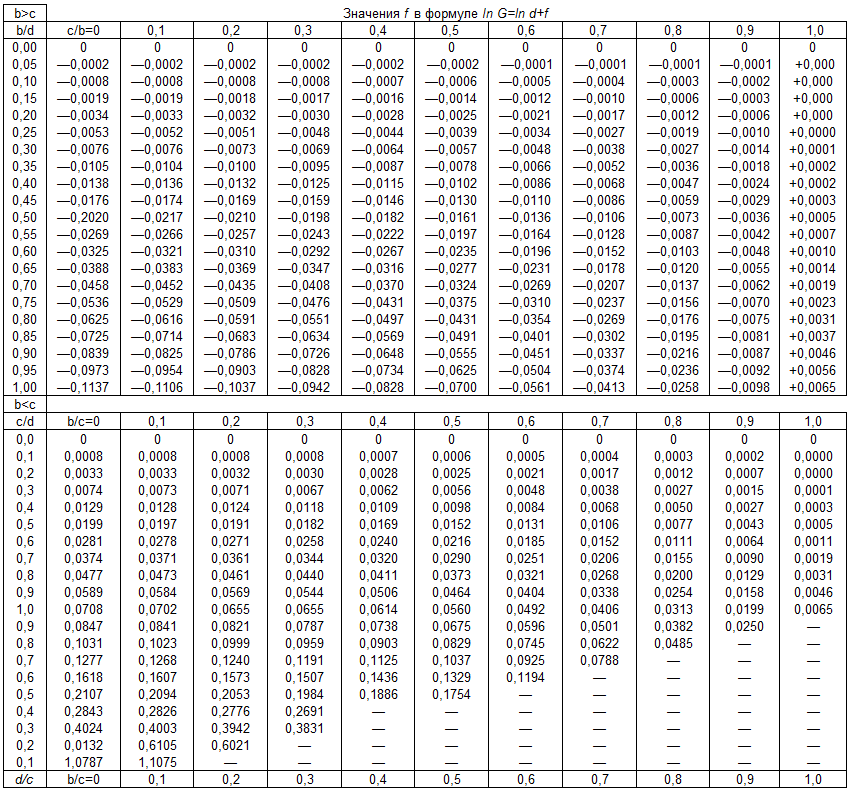
При расположении осей шин по равностороннему треугольнику, т. е. для случая, когда
реактивное сопротивление шинопровода будет равно:
Из формул (10-8) и (10-9) при f = 50 Гц, l — 1 км находим:
где d — расстояние между осями фаз, см.
При расположении осей шин в одной плоскости (вертикально или горизонтально) и расстояниях между осями фаз 1—2 и 2—3 равных d, а между осями фаз 1—3 2d
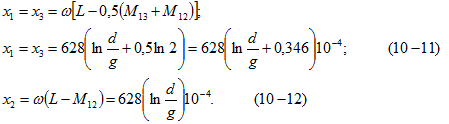
При расположении осей фаз шинопровода в одной плоскости из-за неодинаковости взаимоиндукции между различными парами фаз происходит перенос мощности с одной фазы на другую. Для устранения асимметрии нагрузок при несимметричных шинопроводах применяют транспозицию их фаз. Если же есть необходимость вообще избавиться от проявления эффекта переноса мощности, то прибегают к симметричным токопроводам.
Смотри еще по разделу:
Распределение тока по сечению шин из цветного металла
Определение активного и реактивного сопротивлений шинопровода
Потери мощности и напряжения в шинопроводах
Выбор сечения шинопроводов
Проверка выбранного сечения шинопровода
Колебания шинопроводов, имеющих поворот (отклонение от прямой)