Наведенные напряжения на воздушных линиях при неоднородных трассах сближения - Электромагнитное влияние

• Наведенные напряжения на воздушных линиях при неоднородных трассах сближения
• Электромагнитное влияние
• Электрическое влияние и установки заземлений в месте ремонта

Серия расчетов в схемах с различной степенью детализации схем замещения показала, что для обеспечения достаточной точности результатов не имеет смысла учитывать все неоднородности трасс линий. Для параллельных линий, расположенных на разных опорах, нужно рассматривать только участки длиной не менее нескольких пролетов. Все случаи косого сближения можно сводить к параллельным участкам по методике [7]. Для двухцепных линий необходимо учитывать и более короткие участки, которые часто встречаются на подходах к подстанциям.

Наведенная ЭДС сначала достаточно быстро, а затем достаточно плавно уменьшается (при у1 более 10b24, где b24 - расстояние между крайними фазами ВЛ, спад происходит практически линейно). При этом ошибка в определении у1 на 10-20% слабо изменяет результат. Это существенно при проведении массовых расчетов, так как трассы сближения обычно известны лишь приближенно.

Рассмотрим следующие режимы для РЛ и ВЛ без транспозиций:

а) сопротивление заземлений по концам сравнимо или больше собственного продольного сопротивления проводов (относительно короткие линии и повышенные сопротивления контуров оконечных подстанций);

б) сопротивления контуров подстанций (R1 и R2) много меньше сопротивления проводов.

В первом случае суммарная продольная ЭДС в произвольной точке линии определяется как U1(x) = E1внх , где х - текущая координата вдоль линии, а точка х = 0 принята в месте заземления линии. Тогда график напряжений относительно земли представит собой прямую с наклоном Е1вн . Максимальное напряжение на изолированном конце РЛ составит в рассматриваемом примере при сближении на 40 м: Евн1l =Е™1= 1,5 кВ. Это предельное значение напряжения при R2 —> на втором конце линии.

Случай 2а с точки зрения процессов в РЛ приближается к изолированной линии.

В случае 26 в РЛ возникает значительный встречный ток, компенсирующий влияние Евн. А при наличии встречного тока в РЛ разность напряжений между двумя произвольными точками х1 и х2 на участке, подверженном влиянию, будет меньше Евн на величину падения напряжения на данном участке, вызванного указанным током.

С учетом этого обстоятельства можно сразу сказать, что при R1 —> 0 и R2 —> 0 наведенное напряжение на любом участке и на всей РЛ при сближении однородных линий по всей длине будет равно нулю, так как будет всегда выполняться равенство Евн12 -UIxl2.

Если же сближение происходит на половине длины линии (для определенности от х1 = 0 до х2 = 1/2). Ток в линии определится как Iрл =Eвнl|2 где Z - сопротивление провода всей линии, а не ее половины. Падение напряжения на второй половине линии будетгде Zl/2 = Zl|2 - сопротивление половины длины линии. Падение напряжения между серединой линии и контуром подстанции, созданное током Iрл, будетВнешняя ЭДС на этом участке отсутствует, поэтому Ul|2 определит наведенное напряжение относительно земли. Отсюда в [3] сделан правильный вывод, что наличие внешней ЭДС на половине длины линии является наиболее опасным случаем при глухом заземлении линии по концам.

Теперь рассмотрим наведенные напряжения при полном цикле транспозиций на влияющей линии. Будем считать, что транспозиции сделаны на расстояниях 1/3 и 2l/3 ВЛ общей длиной I. Ремонтируемая линия по-прежнему идет вдоль всей ВЛ параллельно ей и не имеет транспозиций. При симметричной нагрузке в ВЛ на каждом из трех участков сближения наведенные продольные ЭДС будут равны друг другу по модулю и сдвинуты на 120° или в комплексной форме (полагая фазу ЭДС на первом участке равной нулю)

где Е1, Е2 и Е3 - суммарные ЭДС на каждом из участков, т.е. E1-3|

Примем модули |1|, |Е2| и |Е3| равными единице. Длину каждого участка также примем единичной. Общая длина линии теперь равна 1=3. Ясно, что суммарная наведенная ЭДС равна нулю. Следовательно, равен нулю и ток в линии. Поэтому напряжения на РЛ не будут зависеть от сопротивлений заземлений по концам.

Рассмотрим нарастание внешней ЭДС от точки х = 0. Эпюра U(х ) показана на рис. 2. На первом участке (0 <х < 1) происходит линейный рост напряжения, полностью аналогичный случаю линии, заземленной только на одном конце (ток в РЛ равен нулю). Поэтому при х = 1 наведенное напряжение будет равно 1/3 максимальной ЭДС, рассчитанной для сближения однородных линий по всей длине и заземлении при х = 0. Исходя из предыдущего ясно, что это максимальное значение при длинных участках между транспозициями может многократно превысить допустимое.

На среднем участке ЭДС будет определяться суммой двух векторов, сдвинутых на 120°. Первый вектор, определяемый начальным участком РЛ, остается постоянным. Второй линейно растет по мере увеличения х от 1 до 2. На середине этого участка сумма двух векторов в относительных координатах дает значение | U| = cos 30° = 3/2 = 0,866, что следует из рассмотрения треугольников на рис. 2.

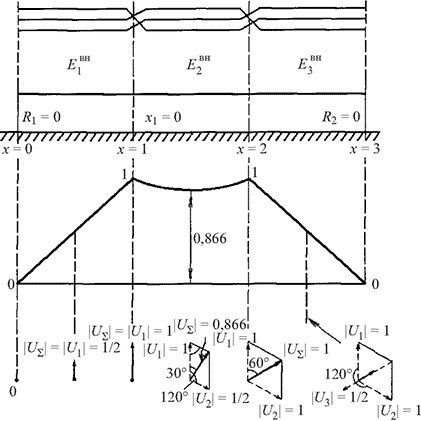
Рис. 2. Распределение наведенных напряжений при транспозициях на влияющей линии (электромагнитное влияние):

Эта ЭДС является минимальной на втором участке, где х1 - координата, отсчитываемая от середины линии (х1 = х- 3/2). К концу второго участка сумма векторов снова дает 1, но вектор суммарной ЭДС повернут относительно ЭДС в начале этого участка на 60°.

Продольная ЭДС на третьем участке будет в противофазе к суммарной ЭДС в конце второго участка. Поэтому по мере увеличения х от 2 до 3 происходит линейный спад напряжения до значения U(x) = 0 при х = 3.

Рассмотренный случай - один из наиболее опасных. Транспозиции на РЛ при отсутствии их на ВЛ влияют значительно слабее. Их влияние определяется только изменением взаимных сопротивлений из-за различных расстояний сближения между ВЛ и расчетным проводом РЛ. Поскольку эти сопротивления медленно спадают с увеличением у1, то и наведенные напряжения (по направлению векторов почти совпадающие на разных участках) будут относительно близки.