Методы повышения долговечности электросетевых конструкций - Целевая функция, ограничения и оптимизационный алгоритм Методы повышения долговечности электросетевых конструкций

Страница 3 из 4

Оптимизация конструкций опор ВЛ может производится отдельно по критериям минимальной массы, минимальной стоимости в деле (по стоимости изготовления, транспортировки и монтажа конструкций), а также по критерию стоимости с учетом эксплуатационных затрат. При выборе оптимального варианта в функцию цели не включаются статьи затрат, одинаковые для конкурирующих значений. Анализ структуры ВЛ свидетельствует о том, что при оптимизационном расчете в составе общей стоимости достаточно учитывать стоимость опор и изоляторов, при расчете по массе — массу опор.

Переходя к целевой функции, остановимся на вопросе оптимизации пролета. От расстояния между опорами зависят основные нагрузки на них: от ветра и гололеда на провода, тяжение провода (троса) при обрыве. Для того, чтобы пересчитать нагрузки в зависимости от величины пролета при варьировании последнего требуется составление достаточно сложных алгоритмов и программ, отражающих все особенности механического расчета проводов. Поэтому изменялись параметры самой конструкции, нагрузки же подсчитывались при фиксированных значениях пролета и задавались как исходные данные. Проводились оптимизационные расчеты для различных значений пролета (и собственно нагрузок и высоты), выбирался оптимальный пролет и соответствующие параметры конструкции. При этом варьирование пролета осуществлялось целенаправленно, с использованием метода одномерной оптимизации для обнаружения экстремума функции одной переменной — поиск делением пополам.

Для определения стрел провеса и напряжения в проводах использовалось уравнение состояния для расчета провода с учетом трех критических пролетов . Провода рассчитывались по семи режимам, требуемым нормами.

Целевая функция формируется алгоритмически в зависимости от переменных, которыми являются геометрические параметры опоры и факторы, характеризующие агрессивность атмосферы.

Основные этапы вычислений целевой функции при оптимизационных расчетах по критерию стоимости с учетом эксплуатационных затрат изложены в разделе 5.4.1.

Схема алгоритма вычисления стоимости конструкции с учетом эксплуатационных затрат приведена на рис. 9.

При вычислении целевой функции удовлетворяются ограничения по несущей способности стержней (43), конструктивные (44), (45), на значения варьируемых параметров (46), а также условия равновесия (47) и совместности деформаций (48).

Анализ задачи оптимизации приводит к выводу, что целевая функция и система ограничений являются сложными нелинейными функциями параметров управления. Велико и число варьируемых параметров (для одностоечной опоры башенного типа насчитывается 20 неизвестных, изменяющихся непрерывно).

Решение таких задач в настоящее время ограничено возможностями математического аппарата счета, поэтому следует стремиться к выбору инженерных методов оптимизационного расчета. Оптимизация опор ВЛ ведется целенаправленным перебором варьируемых параметров. На каждом шаге поиска масса опоры определяется на основе традиционного расчета при удовлетворении требований реального проектирования. Для целенаправленного перебора используется метод деформируемого многогранника.

Ниже изложена последовательность вычислительных операций при оптимизации опор ВЛ с использованием этого метода.

Рис. 14. Последовательность поиска оптимального варианта

Последовательность поиска оптимального варианта

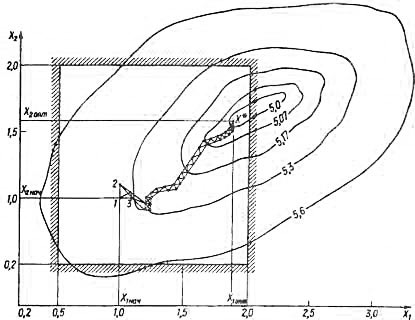
На основе описанного подхода разработан комплекс программ, позволяющий вычислить целевую функцию, а также массу или стоимость опоры в зависимости от варьируемых параметров. Оптимальные параметры находят, задав геометрическую схему конструкции, величину внешних нагрузок и воздействий коррозионной среды. В конце оптимизационного расчета получают рациональную схему конструкции, удовлетворяющую заданному критерию оптимизации.

Задается начальный многогранник, каждая вершина которого описывает конструкцию, отличающуюся хотя бы одним параметром геометрической схемы от остальных. Количество вершин задается на единицу больше количества варьируемых параметров. На рис. 14 показана последовательность поиска оптимального варианта в случае двух неизвестных. Вершина 1 начального треугольника имеет координаты, соответствующие параметрам типовой конструкции. Вершина 2 отличается от них параметром Х2, 3 — параметром Х1. Вычисляются значения целевой функции в вершинах, удовлетворяющие ограничениям, отмечаются максимальная и минимальная величины. Значения целевой функции, удовлетворяющие допустимой области, характеризуются линиями уровня.

Вершина, в которой целевая функция максимальна, переносится определенным образом через центр тяжести многогранника (треугольника для двухмерного случая). Для новых значений варьируемых параметров вычисляется целевая функция, причем если параметры превысили верхний или нижний предел, то принимаются равными этому пределу. Улучшенные (более низкие) значения целевой функции находятся последовательной заменой точки с максимальным значением на точки с более низким значением (рис. 14). Процедура отыскания вершины, в которой функция цели имеет более низкие значения, состоит из операций отражения, растяжения, сжатия и редукции, приспосабливающих процесс поиска к характеру целевой функции. Ограничения (43)— (45) и уравнения связи (47), (48) изменяются в процессе оптимизации при варьировании параметров опоры ВЛ. Поэтому на каждой итерации область допустимых значений меняется, удовлетворение целевой функции этой области достигается расчетом конструкции и подбором сечений при удовлетворении условий равновесия, совместимости деформаций, прочности, устойчивости, конструктивных требований.

Поиск считается оконченным, когда многогранник в области минимума стягивается в точку.