Частотные годографы

Рассмотренные выше круговые диаграммы являются частным случаем геометрических мест концов векторов, изображающих различные физические величины при изменении одного из параметров цепи. Если изменяемым параметром является не сопротивление или емкость элемента цепи, как это было рассмотрено, а частота источника питания цепи переменного тока, то годограф называют частотным. В этом случае форма диаграммы более сложная и только в простейших случаях изображается окружностью или прямой.

К числу таких простейших случаев относится последовательное соединение резистивного, индуктивного и емкостного элементов (последовательный контур), для которого частотный годограф комплексного сопротивления имеет вид прямой, а проводимости - окружность.

Рис. 9.14

Действительно, построив геометрическое место концов векторов или для цепи, изображенной на рис. 3.8, получим прямую и окружность, изображенные на рис. 9.14, а и б. Здесь точка а на годографе соответствует резонансу напряжений при резонансной частоте

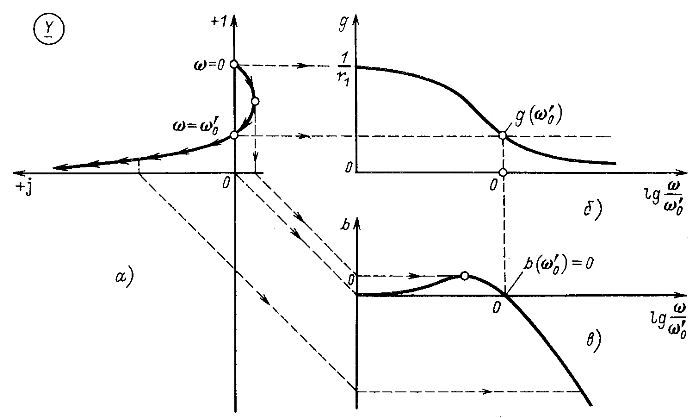
Более сложную форму имеет частотный годограф для комплексных сопротивления и проводимости параллельного соединения индуктивного и емкостного элементов при учете активного сопротивления одного из элементов параллельного контура. Так, например, цепь имеет частотный годограф, существенно отличающийся от прямой или окружности. На рис. 9.15, а изображен частотный годограф при для комплексной проводимости цепи

Рис. 9.15

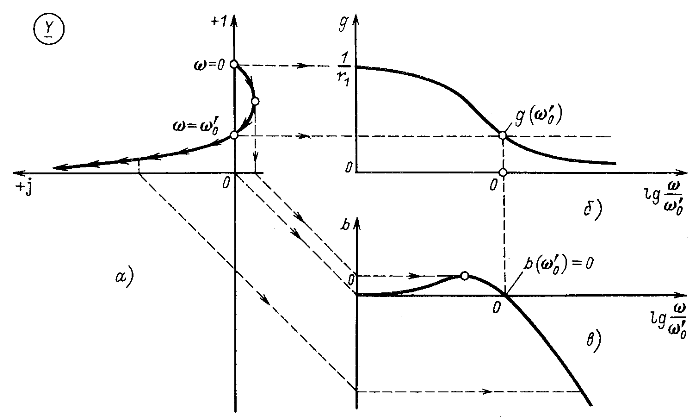
На рис. 9.15, б и в построены частотные характеристики активной и реактивной составляющих комплексной проводимости цепи:

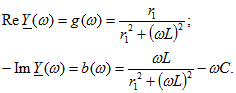
Интересно отметить, что резонанс наступает при частоте [ cм. (5.14)], отличной от частоты, при которой имеет место минимум полной проводимости цепи у:

Частотные годографы получили широкое распространение в автоматике при описании частотных характеристик передаточных функций различных электрических, электронных и электромеханических четырехполюсников.

Дополнительно по теме