Резонанс в цепи несинусоидального тока

При несинусоидальных напряжениях и токах явление резонанса усложняется, так как возможны отдельные резонансы гармонических составляющих.

Предположим, что источник несинусоидального напряжения, состоящего из трех гармоник, подключен к последовательному контуру (рис. 12.19).

Ток каждой из гармоник

Если, например, индуктивность L изменять от нуля до бесконечности, то действующее значение каждой из составляющих тока будет изменяться по резонансной кривой от при L = 0 до при и далее будет снижаться до нуля при .

Рис. 12.19

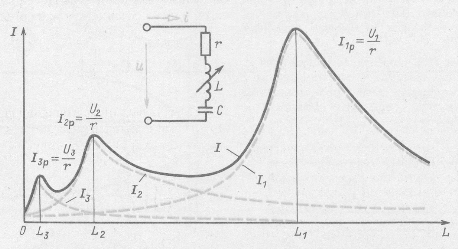
На рис. 12.19 штриховой линией построены резонансные кривые для трех гармонических составляющих периодического несинусоидального тока. Значения индуктивности L при резонансах обратно пропорциональны квадрату номера гармоники:

Кривая общего действующего тока

при достаточно малом r имеет три резко выраженных максимума, соответствующих резонансным значениям индуктивности.

Аналогичные зависимости получаются и при изменении емкости или частоты, если, конечно, в последнем случае форма кривой напряжения остается неизменной.

В цепях, содержащих источники несинусоидальных ЭДС и токов, резонансные явления могут применяться для выделения требуемых частот и, наоборот, для подавления нежелательных частот.

Пример 12.10.

Несинусоидальное напряжение

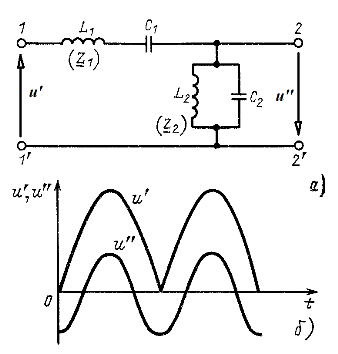
Несинусоидальное напряжение u' на выводах 1-1' четырехполюсника (рис. 12.20, а) получено в результате двух-полупериодного выпрямления синусоидального напряжения с угловой частотой w (см. приложение 3, строка 9).

Последовательный контур и параллельный настроены в резонанс на 2-ю гармонику 2w, т. е. .

Найти действующее значение напряжения u" на выводах 2-2' и коэффициент искажения в режиме холостого хода при следующих параметрах: .

Рис. 12.20

Решение. В напряжении u" выделяется 2-я гармоника, так как для нее сопротивление последовательного контура и проводимость параллельного контура равны нулю, в то время как для всех остальных гармоник соответствующие сопротивление и проводимость конечны и растут с номером гармоники.

В режиме холостого хода, как следует из рис. 12.20, а, для каждой гармоники где

Разложив напряжение u' в ряд по формуле, приведенной в строке 9 приложения 3, получим, что постоянная составляющая u" равна нулю (постоянного тока в последовательном контуре нет), 1 -й гармоники u" нет, так как ее не содержит напряжение u' (нет и всех высших нечетных гармоник).

Для 2-й гармоники , а , поэтому напряжения на входе и выходе четырехполюсника одинаковы: .

Для 4-й гармоники , и, следовательно, .

Для 6-й гармоники и .

Восьмой и более высокими гармониками можно пренебречь.

Таким образом, действующее напряжение на вторичных выводах

действующее напряжение основной (2-й) гармоники , и коэффициент искажения .

В целях улучшения формы кривой u" целесообразно включить параллельно контуру конденсатор и обеспечить для напряжения 4-й гармоники резонанс токов в контуре при . В этом случае для 4-й гармоники , и, следовательно, .

Для 6-й гармоники и получается .

Действующее напряжение , и коэффициент искажения (рис. 12.20, б).

Такая схема представляет собой частный случай полосового фильтра и может быть применена для увеличения частоты вдвое (умножитель частоты). На аналогичном принципе основываются утроители частоты и умножители частоты большей кратности.

Несинусоидальное напряжение

Дополнительно по теме