Резонанс токов

1. Для контура (рис. 5.31) параметры которого равны: определить, чему равны эквивалентные резистивное, реактивное и полное сопротивления контура, если вследствие расстройки частота станет на 0,2% больше резонансной. Для этого случая вычислить все токи и мощность, выделяемую полагая, что значение приложенного к цепи осталось прежним (U=200 В).

Решение:
Вначале определим добротность Q и сопротивление контура при резонансе:

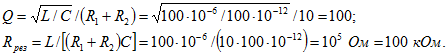Произведем расчеты при . Найдем абсолютную и обобщенную расстройки и искомые сопротивления: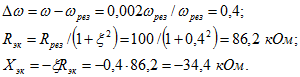 имеет емкостный характер, так как x, положительно.
Полное сопротивление при расстройке

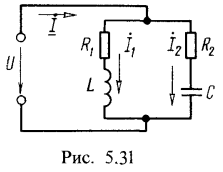
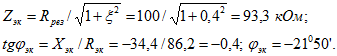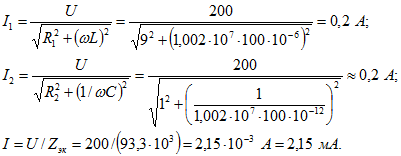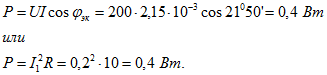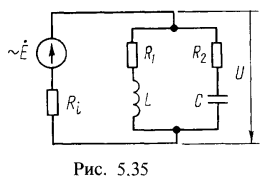
Так как отрицательно, ток опережает напряжение Расходуемая мощность Заметим, что даже при небольшой расстройке (0,2%) в полном сопротивлении контура появилась значительная реактивная составляющая , вследствие которой и оказался сдвиг фаз между током I и напряжением U. Ввиду небольшого изменения частоты реактивные сопротивления каждой из параллельных ветвей и токи в них почти не изменились и не намного изменился ток в неразветвленной части цепи.2. Параллельный контур с малыми потерями (т. е. Q>>1) включен к источнику с ЭДС Е=200 В и внутренним сопротивлением (см. рис. 5.35). Определить параметры контура R и L, если известны резонансная частота , емкость С=300 пФ и что сопротивление контура при резонансе равно внутреннему сопротивлению генератора . Вычислить токи источника, каждой из ветвей, мощность, доставляемую источником, и выделяемую в нем и в параллельном контуре при резонансе.Решение:
Находим индуктивность: Имея в виду, что по условию находим резистивное сопротивление

Ток источника и напряжение на параллельном контуре при резонансе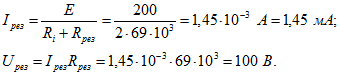 В каждой из ветвей контура токи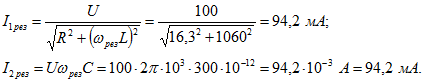

Мощность, доставляемая источником , расходуемая в нем и выделяемая в контуре : 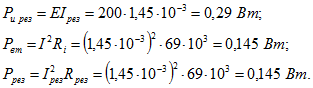3. Для задачи 2. определить абсолютное значение и относительную величину полосы пропускания контура по напряжению.Решение:
Предварительно вычислим характеристическое сопротивление и добротность контура Искомые значения абсолютной и относительной величины полосы пропускания контура по напряжению равны: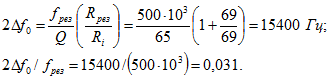

4. Параллельный контур, параметры которого , подключен к источнику с ЭДС Е=200 В и внутренним сопротивлением .
1. Вычислить эквивалентную добротность контура и полосу его пропускания. Найти все токи и расходуемую в контуре мощность при резонансе.
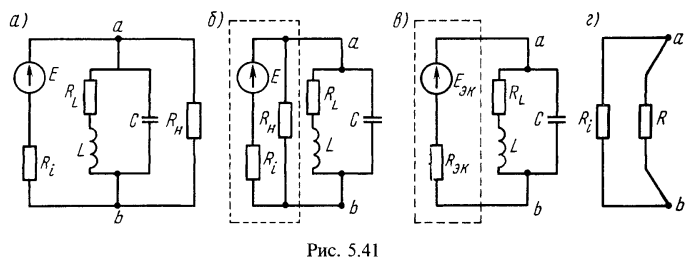
2. Чему равны эквивалентная добротность контура и полоса его пропускания, если его нагрузить на резистивное сопротивление (рис. 5.41, а)? Определить для данного случая токи, мощности, доставляемую источником и расходуемую в контуре и нагрузочном сопротивлении при резонансе.

Решение:
1. Для заданного контура вычисляем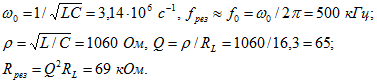 Эквивалентную добротность заданного контура с учетом внутреннего сопротивления источника ЭДС и полосу его пропускания определяем:
Так как данные контура, ЭДС источника и его внутреннего сопротивления те же, что и в задаче 2., то в решении были уже вычислены требуемые по условию
2. Решение задачи в случае нагрузки контура на сопротивление проще всего получить, осуществив замену относительно зажимов ab заданного источника ЭДС с и подключенным к нему параллельно сопротивлением (рис. 5.41, б), эквивалентным с ЭДС и внутренним сопротивлением (рис. 5.41,в). Для определения отключим параллельный контур (см. рис. 5.41,б и в) и вычислим напряжение холостого хода равное : Сопротивление короткого замыкания равно внутреннему сопротивлению эквивалентного источника (рис. 5.41,г): Для схемы рис. 5.41 эквивалентные добротность и полоса пропускания соответственно равны Следует отметить, что подключение к контуру сопротивления приводит к уменьшению эквивалентной добротности и увеличению полосы пропускания.
Рассчитываем ток в неразветвленной части заданной цепи, напряжение на контуре, токи в ветвях контура и нагрузочном сопротивлении , мощности, доставляемую источником и выделяемую в контуре и сопротивлении : 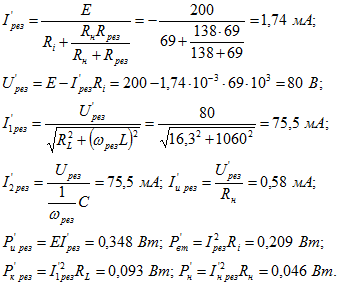Проверка показывает, что

Смотри полное содержание по представленным решенным задачам.