Трехфазные цепи (страница 2)

ТРЕХФАЗНЫЕ ЦЕПИ

10. К трехпроводной трехфазной цепи с линейными напряжениями 120 В присоединена электрическая лампа мощностью 60 Вт.
Определить токи в проводах трехфазной линии.Решение:
Пусть лампа присоединена к проводам А и В. По условию задачи, . Напряжение такой величины действует между зажимами лампы, представляющей собой приемник энергии, для которого .
Ток в лампе определяется из формулы мощности: В линейном проводе С ток отсутствует, ток будет проходить лишь в линейных проводах А и В, в которых он равен току . Однако если нас интересует сдвиг фаз токов относительно отдельных напряжений трехфазной системы, то следует обратиться к векторной диаграмме. Ток как ток в активном сопротивлении совпадает по фазе с напряжением а вектор этого тока на диаграмме совпадает по направлению с вектором напряжения (рис. 49); диаграмма построена в масштабе: .
На электрической схеме всегда указывают положительные направления токов и напряжений, т. е. направления для положительной половины периода каждой из этих величин. За положительные направления токов в проводах линии принимают всегда направления к приемнику (см. рис. 49).

На основании первого закона Кирхгофа имеем:
для точки узловой А

для точки узловой В откуда т. е. один и тот же вектор изображает как ток лампы так и ток , так и ток в проводе А.

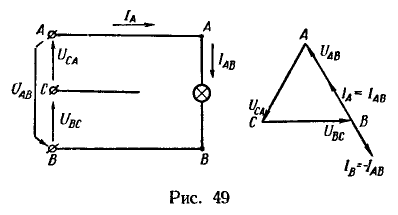
Далее, вектор тока в проводе В противоположен по направлению вектору тока лампы , но имеет одинаковую с ним длину. Это отражено на рисунке к данной задаче.
Номинальное расчетное напряжение лампы должно быть равно линейному напряжению, чтобы лампа работала нормально и давала гарантированный заводом световой поток.11. Однофазный трансформатор присоединен к проводам В и С трехпроводной трехфазной цепи с линейным напряжением 220 В. Ток трансформатора составляет 10 А и отстает по фазе от напряжения на 1/12 периода.
Построить векторную диаграмму.Решение:
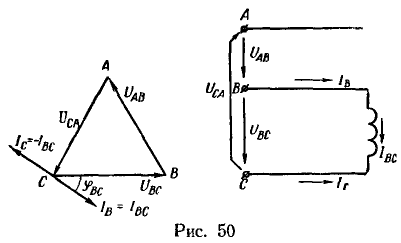
Построение диаграммы начинаем с равностороннего треугольника линейных напряжений в масштабе (рис. 50). Так как, по условию задачи, трансформатор включен на линейное напряжение , то его первичный ток отстает по фазе на 1/12 периода (т. е. 30°) от линейного напряжения . Для токов выбираем масштаб . При построении угла сдвига учитываем, что вектор напряжения вращается вокруг своего начала (точка С) против часовой стрелки.

На основании первого закона Кирхгофа имеем:
для узловой точки В

для узловой точки С

Спедовательно, ток в проводе В изображается тем же
вектором, что и ток , а ток — противоположно направленным вектором.

12. Между проводами А и В трехпроводной трехфазной цепи включены 21 электрическая лампа мощностью 40 Вт каждая, а между проводами С и А — 10 ламп мощностью 60 Вт каждая.
Определить токи в линейных проводах и построить в масштабе векторную диаграмму, если линейные напряжения равны 120 В.Решение:
Мощность электрических ламп, включенных между проводами АВ, Мощность электрических ламп, включенных между проводами С и А, Каждая из этих групп ламп представляет так называемую фазу или сторону треугольника нагрузки. Суммарные токи каждой из групп ламп представляют фазные токи (или токи в сторонах треугольника):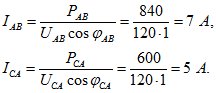

При вычислениях учтено, что для электрических ламп . Чтобы установить связь между фазными и линейными токами, обратимся к электрической схеме цепи (рис. 51, а), согласно которой имеем:
для узловой точки С для узловой точки В для узловой точки А

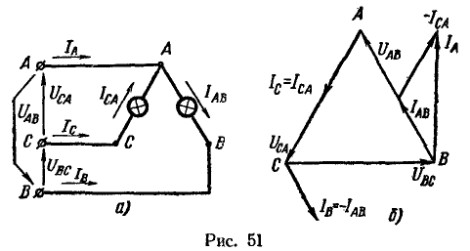
Вычитание векторов можно свести к сложению. При этом к вектору следует прибавить вектор , предварительно повернув его на 180° и получив вектор .
Сложение векторов выполнено по правилу многоугольника, когда к концу одного вектора пристраивают начало другого вектора.
Диаграмма на рис. 51, б построена в масштабе: . Непосредственное измерение длины вектора на диаграмме дает величину тока (отрезок длиной 47 мм).
Линейные токи равны по величине фазным токам , как следует из рис. 51, а и уравнений. Если необходимо определить углы сдвига фаз токов относительно напряжений, то это можно сделать при помощи транспортира, измерив углы между соответствующими векторами на диаграмме, вычерченной в достаточно крупном масштабе.13. Обмотки трехфазного асинхронного электродвигателя соединены треугольником. Электродвигатель присоединен к трехпроводной трехфазной цепи с линейными напряжениями 220 В, причем мощность на валу электродвигателя равна 28,47 кВт, к. п. д. и коэффициент мощности .
Определить фазные и линейные токи, построить в масштабе векторную диаграмму.Решение:
При номинальной мощности на валу и к. п. д. мощность на входе Трехфазный электродвигатель является симметричной нагрузкой, для которой справедлива следующая формула мощности: где U и I — линейные значения напряжения и тока;
— угол сдвига фаз между напряжением и током.
Из этой формулы определяем линейный ток:

При симметричной нагрузке ток такой величины проходит в каждом линейном проводе , а в каждой стороне треугольника (в каждой фазе) он в раз меньше: Из таблиц тригонометрических величин (определены по значению коэффициента мощности).

На такие же углы сдвинуты в сторону отставания фазные токи от соответствующих фазных напряжений (при схеме соединения треугольником фазные напряжения являются также линейными напряжениями). При симметричном режиме цепи в схеме соединения треугольником линейные токи сдвинуты на углы 30° от фазных токов.
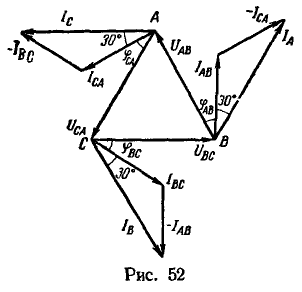
Векторная диаграмма построена в масштабе: . Как видно из рис. 52, векторная диаграмма представляет равносторонний треугольник линейных напряжений, около вершин которого расположены равнобедренные треугольники токов. Каждый угол при основаиии этих треугольников равен 30°, а основанием для них является вектор линейного тока (соответственно ).

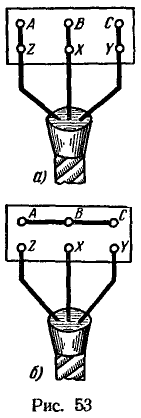
14. Соединение зажимов обмоток трехфазного асинхронного электродвигателя на клеммной дощечке было выполнено так, как показано на рис.53, a, а электромонтер заменил это соединение таким, как изображено на рис. 53, б.
Определить изменение напряжений на фазных обмотках электродвигателя, если линейные напряжения сети равны 380 В.Решение:
Соединение зажимов по рис. 53, а соответствует соединению обмоток треугольником. При этом соединении пара линейных проводов присоединяется непосредственно к зажимам фазной обмотки, и линейное напряжение Соединение зажимов по рис. 53, б соответствует соединению обмоток звездой. При этом соединении фазное напряжение обмотки в раз меньше, чем напряжение между двумя линейными проводами, так как трехфазный электродвигатель — симметричный приемник энергии: В обеих схемах напряжение трехфазной сети было одно и то же, т. е. в результате замены соединения зажимов обмоток электродвигателя напряжения на них уменьшились в раз.

15. К четырехпроводной трехфазной цепи с линейными напряжениями 220 В параллельно подключены осветительные установки двух помещений: в одной из них лампы соединены треугольником, причем мощность в каждой фазе 2,2 кВт, в другой — звездой с нейтральным проводом, причем мощность в каждой фазе 1,27 кВт.
Определить токи на всех участках схемы.Решение:
В схеме соединения треугольником напряжение на каждой фазе ламп равно линейному напряжению, т. е. .
Ток в каждой фазе, например в фазе, включенной между проводами А и В, где для ламповой нагрузки . Такой же величины токи проходят в фазах ВС и С А.
Ток в каждом линейном проводе, присоединенном к вершине треугольника, в раз больше фазного тока, так как нагрузка фаз равномерная. Например, . Такой же величины токи проходят в проводах В и С.
Каждый из токов , проходящих в фазах треугольника, совпадает соответственно с напряжениями , так как при ламповой нагрузке сдвига фаз нет.
Линейные токи при равномерной нагрузке фаз приемника, соединенного треугольником, отстают от соответствующих фазных токов на углы 30°, например ток отстает от тока на угол 30°.
С другой стороны, линейное напряжение, например напряжение опережает на угол 30° фазное напряжение при соединении звездой. Следовательно, ток , отставая по фазе на угол 30° от фазного тока (совпадающего в свою очередь по фазе с напряжением ), будет совпадать по фазе с напряжением (фазным для схемы соединения звездой). Поэтому ток в фазе А схемы соединения звездой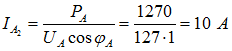 арифметически складывается с током . В линейном проводе А до разветвления между двумя осветительными установками будет проходить суммарный ток Так как, по условию задачи, нагрузка равномерная в обеих осветительных установках, то результаты расчета, выполненного для фазы А, следует распространить на фазы В и С.
Итак, токи в линейных проводах установки, соединенной треугольником, , а в линейных проводах установки, соединенной звездой, Токи в линейных проводах до разветвления между осветительными установками .
В нейтральном проводе ток отсутствует, так как нагрузка в схеме соединения звездой симметричная. При решении задачи нам удалось обойтись без построения векторной диаграммы благодаря чисто активной нагрузке обоих приемников. Сдвиги между фазными напряжениями установок равны сдвигам между фазными токами.

Смотри полное содержание по представленным решенным задачам.