Трехфазные цепи (страница 1)
Трехфазные цепи (страница 1)
ТРЕХФАЗНЫЕ ЦЕПИ
1. Линейное напряжение трехфазного генератора, соединенного звездой, равно 10500 В.
Определить напряжение между зажимами каждой фазы генератора. Какое напряжение было бы между зажимами генератора при соединении его обмоток треугольником?
Решение:
Фазное напряжение трехфазного генератора при схеме соединения звездой в ![]() раз меньше линейного напряжения:
раз меньше линейного напряжения:
![]()
В схеме соединения треугольником провода линии присоединяются к общим зажимам двух обмоток, и линейное напряжение между двумя проводами равно напряжению фазной обмотки:![]()
2. Действующее значение э. д. с. в каждой обмотке симметричного трехфазного генератора равно 230 В.
Определить линейные напряжения при соединении обмоток неправильной звездой («веером») в режиме холостого хода.Решение:
Неправильное присоединение одной из обмоток генератора к двум остальным при соединении звездой приводит к повороту вектора э. д. с. на 180° (рис. 35) по сравнению с нормальным расположением. Вместо симметричной трехлучевой звезды векторов получается так называемый веер векторов с углами по 60° между ними. Как видно из векторной диаграммы, напряжение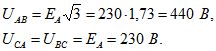 Следовательно, неправильное соединение обмоток звездой можно обнаружить путем измерения. При правильном соединении все линейные напряжения равны
Следовательно, неправильное соединение обмоток звездой можно обнаружить путем измерения. При правильном соединении все линейные напряжения равны ![]() .
.
3. В каждой обмотке трехфазного генератора индуктируется э. д. с, равная 132 В.
Определить линейное напряжение генератора при холостом ходе в случае соединения обмоток треугольником.Решение:
При правильном соединении обмоток трехфазного генератора треугольником результирующая э. д. с. в контуре обмоток равна нулю, так как сумма э. д. с. симметричной трехфазной системы равна нулю. Следовательно, при холостом ходе в контуре треугольника обмоток ток отсутствует и напряжение между концом и началом обмотки равно э. д. с. Это так называемое фазное напряжение. В схеме соединения генератора треугольником провода трехфазной линии присоединяют к точкам соединения обмоток. Каждый провод при этом присоединен к зажимам двух обмоток, а каждая пара проводов линии — к зажимам одной из трех обмоток. Поэтому линейное напряжение генератора, т. е. напряжение между двумя линейными проводами, оказывается равным при схеме соединения треугольником фазному напряжению, а при холостом ходе генератора — фазной э. д. с. генератора (132 В).4. Фазная э, д. с. трехфазного генератора Е=247 В, частота сети f=50 Гц, активное сопротивление обмотки r=1,1 Ом, индуктивное сопротивление ![]() .
.
Определить величину тока в контуре треугольника при неправильном соединении обмоток генератора в режиме холостого хода.Решение:
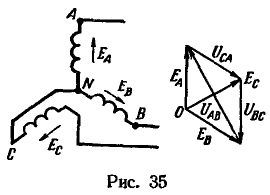
Переключение начала и конца обмотки трехфазного генератора поворачивает вектор э. д. с. этой обмотки на диаграмме на 180°. Дело в том, что после переключения положительное направление э. д. с. этой обмотки будет относительно зажимов остальных обмоток таким, каким было отрицательное направление э. д. с. в первоначальной схеме. Таким образом, при неправильном соединении, например, фазы В по отношению к остальным фазам получим векторную диаграмму, показанную на рис. 36.
Результирующая э. д. с. в контуре равна удвоенному значению фазной э. д. с, т. е. 494 В. Эта э. д. с. обусловливает ток в контуре, величина которого определяется по закону Ома:![]() где z — полное сопротивление фазной обмотки:
где z — полное сопротивление фазной обмотки:![]() Следовательно,
Следовательно,![]()
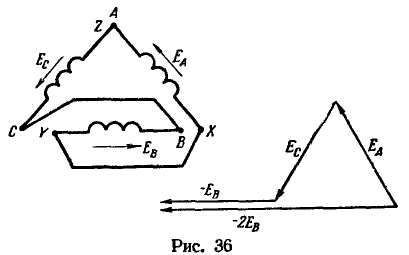
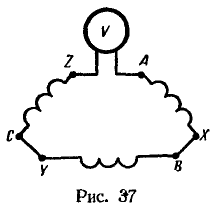
Если оставить включенной схему неправильного соединения обмоток треугольником, то даже при холостом ходе генератора в контуре обмоток будет непроизводительно расходоваться энергия, переходящая в тепло. В рассматриваемой задаче потери мощности в контуре![]() Поэтому, прежде чем замыкать контур треугольника обмоток, следует проверить равнопотенциальность соединяемых точек при помощи вольтметра (рис. 37). При правильном соединении обмоток треугольником подвижная часть вольтметра не отклоняется.
Поэтому, прежде чем замыкать контур треугольника обмоток, следует проверить равнопотенциальность соединяемых точек при помощи вольтметра (рис. 37). При правильном соединении обмоток треугольником подвижная часть вольтметра не отклоняется.
5. К четырехпроводной трехфазной линии поочередно присоединяют три электрические лампы мощностью по 60 Вт каждая между линейным (соответственно А, В и С) и нейтральным проводами.
Определить изменение токов в проводах линии в каждом случае присоединения к ней ламп, если напряжение между каждым линейным проводом и нейтральным проводом 120 В.Решение:
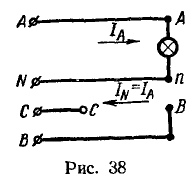
Пусть до присоединения к четырехпроводной трехфазной линии ламп в ее проводах не было токов. Тогда присоединение электрической лампы между линейным А и нейтральным N проводами вызовет ток в этих проводах, равный![]() Благодаря нейтральному проводу поддерживаются равными три фазных напряжения:
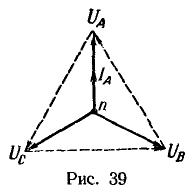
Благодаря нейтральному проводу поддерживаются равными три фазных напряжения: ![]() и на векторной диаграмме узловой точке n цепи (рис. 38) соответствует точка того же наименования, расположенная в центре тяжести треугольника векторов линейных напряжений (рис. 39).
и на векторной диаграмме узловой точке n цепи (рис. 38) соответствует точка того же наименования, расположенная в центре тяжести треугольника векторов линейных напряжений (рис. 39).
Электрическая лампа является однофазным приемником энергии, не вызывающим сдвига фаз тока относительно напряжения ![]() . Следовательно, вектор тока
. Следовательно, вектор тока ![]() совпадает по фазе с вектором напряжения
совпадает по фазе с вектором напряжения ![]() . Согласно первому закону Кирхгофа, примененному к точке n цепи (рис. 39), ток в нейтральном проводе
. Согласно первому закону Кирхгофа, примененному к точке n цепи (рис. 39), ток в нейтральном проводе ![]() изображается тем же вектором, что и ток в проводе А. Из этого рисунка видно, что при отсутствии нейтрального провода лампу нельзя было бы включить на фазное напряжение
изображается тем же вектором, что и ток в проводе А. Из этого рисунка видно, что при отсутствии нейтрального провода лампу нельзя было бы включить на фазное напряжение ![]() .
.
Представим себе, что в дополнение к уже включенной лампе (см. рис. 38) присоединена вторая такая же лампа между линейным В и нейтральным N проводами (рис. 40).
Ток в проводе А при этом не изменился, но появился ток в проводе В. В нейтральном проводе N стал проходить ток ![]() , равный геометрической сумме токов
, равный геометрической сумме токов ![]() .
.
Ток в линейном проводе В![]() Он совпадает по фазе с напряжением
Он совпадает по фазе с напряжением ![]() и тем самым отстает по фазе от тока
и тем самым отстает по фазе от тока ![]() на 1/3 периода (120°) (см. рис. 40).
на 1/3 периода (120°) (см. рис. 40).
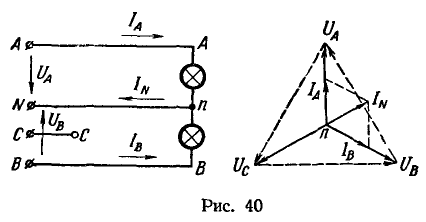
Так как ![]() , то при определении тока в нейтральном проводе путем сложения векторов этих линейных токов получим ромб с углом в 120°. Диагональ ромба
, то при определении тока в нейтральном проводе путем сложения векторов этих линейных токов получим ромб с углом в 120°. Диагональ ромба ![]() делит этот угол пополам, поэтому длина диагонали ромба равна его стороне, т. е.
делит этот угол пополам, поэтому длина диагонали ромба равна его стороне, т. е.![]() Таким образом, величина тока в нейтральном проводе осталась той же, что и при одной лампе в проводе А, только вектор этого тока на диаграмме повернулся на 60° по ходу часовой стрелки.
Таким образом, величина тока в нейтральном проводе осталась той же, что и при одной лампе в проводе А, только вектор этого тока на диаграмме повернулся на 60° по ходу часовой стрелки.
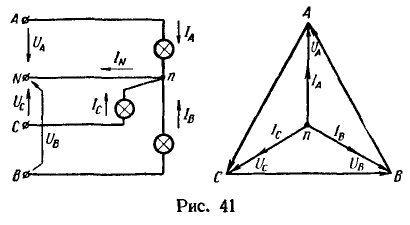
Наконец, допустим, что присоединена третья лампа (в дополнение к прежним двум) между линейным С и нейтральным N проводами (рис. 41). В этом случае ток
![]() стал проходить в проводе С, причем ввиду отсутствия сдвига фаз этого тока относительно напряжения
стал проходить в проводе С, причем ввиду отсутствия сдвига фаз этого тока относительно напряжения ![]() вектор тока
вектор тока ![]() на диаграмме начал совпадать по фазе с вектором напряжения
на диаграмме начал совпадать по фазе с вектором напряжения ![]() .
.
Получилась симметричная трехлучевая звезда векторов токов. Геометрическое сложение этих векторов дает нуль: ![]() . Следовательно, при симметричном режиме нагрузки ток в нейтральном проводе равен нулю.
. Следовательно, при симметричном режиме нагрузки ток в нейтральном проводе равен нулю.
Таким образом, отсутствие тока в нейтральном проводе при однородной (например, активной) нагрузке свидетельствует о симметрии режима в трехфазной цепи.
6. Трехфазный асинхронный электродвигатель типа МАД-126/8 в схеме соединения обмоток статора звездой при номинальной нагрузке и номинальном напряжении 500 В имеет токи в обмотках статора по 220 А и развивает номинальную мощность на валу 130 кВт.
Определить ![]() и мощность на входе, если к. п. д. при номинальной нагрузке
и мощность на входе, если к. п. д. при номинальной нагрузке ![]() . Построить в масштабе векторную диаграмму.
. Построить в масштабе векторную диаграмму.
Решение:
К. п. д. ![]() , откуда
, откуда![]()
Трехфазный электродвигатель — это симметричный приемник энергии, поэтому коэффициент мощности![]() Этому значению коэффициента мощности соответствует угол
Этому значению коэффициента мощности соответствует угол ![]() .
.
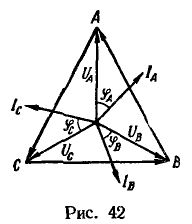
Строим векторную диаграмму в масштабе: ![]() (рис. 42). Так как трехфазный электродвигатель представляет собой симметричный приемник энергии, то геометрическая сумма его токов равна нулю и нейтральный провод становится Лишним. Поэтому при любой схеме соединения обмоток трехфазного двигателя к нему подводят только три провода.
(рис. 42). Так как трехфазный электродвигатель представляет собой симметричный приемник энергии, то геометрическая сумма его токов равна нулю и нейтральный провод становится Лишним. Поэтому при любой схеме соединения обмоток трехфазного двигателя к нему подводят только три провода.
7. Три одинаковые катушки ![]() включены звездой и присоединены к трехпроводной трехфазной цепи с линейным напряжением 220 В. Начало и конец одной из катушек (фаза А) замкнуты накоротко медной пластиной.
включены звездой и присоединены к трехпроводной трехфазной цепи с линейным напряжением 220 В. Начало и конец одной из катушек (фаза А) замкнуты накоротко медной пластиной.
Определить токи при коротком замыкании в фазе А. Построить в масштабе векторную диаграмму.Решение:
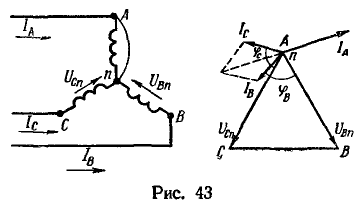
Замыкание накоротко точек A и n (рис. 43) делает потенциал точки n равным потенциалу точки А.
Катушки фаз В и С оказываются включенными на линейное напряжение. Токи в них равны по величине:![]()
Они отстают по фазе соответственно от напряжений ![]() на угол, тангенс которого
на угол, тангенс которого![]() Из таблиц тригонометрических величин
Из таблиц тригонометрических величин ![]() . Ток
. Ток ![]() в замкнутой накоротко фазе А
в замкнутой накоротко фазе А ![]() определяют в этом случае по первому закону Кирхгофа:
определяют в этом случае по первому закону Кирхгофа: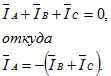 Следовательно, вектор тока
Следовательно, вектор тока ![]() противоположен по направлению вектору, представляющему собой сумму векторов
противоположен по направлению вектору, представляющему собой сумму векторов ![]() . Строим векторную диаграмму масштаба:
. Строим векторную диаграмму масштаба: ![]() .
.
Непосредственное измерение дает для величины тока замкнутой накоротко фазы А значение ![]() .
.
При нормальных условиях токи во всех линейных проводах были бы равны:![]() Поэтому в замкнутой накоротко фазе схемы «симметричная звезда» ток больше, чем при нормальной работе, в 3 раза, при этом в двух других фазах ток увеличивается в
Поэтому в замкнутой накоротко фазе схемы «симметричная звезда» ток больше, чем при нормальной работе, в 3 раза, при этом в двух других фазах ток увеличивается в ![]() раз.
раз.
Ток ![]() замыкается через пластину, замкнувшую зажимы катушки. В этой катушке не может быть пробоя междувитковой изоляции, так как напряжение между зажимами катушки равно нулю. Опаснее для изоляции катушки внезапное прекращение тока, так как при этом в катушке индуктируется очень большая э. д. с. самоиндукции.8. К трехпроводной трехфазной линии напряжением 122 В и частотой 50 Гц присоединены включенные звездой катушки
замыкается через пластину, замкнувшую зажимы катушки. В этой катушке не может быть пробоя междувитковой изоляции, так как напряжение между зажимами катушки равно нулю. Опаснее для изоляции катушки внезапное прекращение тока, так как при этом в катушке индуктируется очень большая э. д. с. самоиндукции.8. К трехпроводной трехфазной линии напряжением 122 В и частотой 50 Гц присоединены включенные звездой катушки ![]() . В проводе С линии расплавилась плавкая вставка предохранителя (рис. 44).
. В проводе С линии расплавилась плавкая вставка предохранителя (рис. 44).
Определить токи. Построить в масштабе векторную диаграмму.
Решение:
Вследствие расплавления плавкой вставки предохранителя ток в линейном проводе С прекратился. Потенциалы точек ![]() и n стали равными.
и n стали равными.
В схеме под действием линейного напряжения ![]() продолжается прохождение тока в катушках фаз А и В, включенных теперь последовательно.
продолжается прохождение тока в катушках фаз А и В, включенных теперь последовательно.
Так как катушки одинаковы, то напряжение ![]() делится между ними поровну.
делится между ними поровну.
Это означает, что точка n диаграммы находится посередине вектора линейного напряжения ![]() . Отрезок An означает напряжение
. Отрезок An означает напряжение ![]() , а отрезок Вn — напряжение
, а отрезок Вn — напряжение ![]() .
.
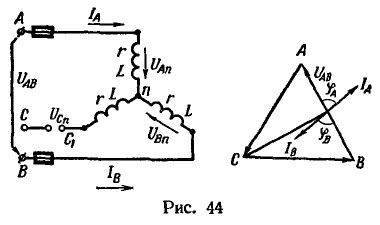
Симметричная трехлучевая звезда векторов фазных напряжений, которая характеризовала симметричный режим при всех исправных предохранителях, искажается ввиду смещения точки n из центра тяжести треугольника линейных напряжений на середину стороны АВ (см. рис. 44). Токи ![]() равны по величине:
равны по величине:
![]() Они отстают по фазе соответственно от напряжений
Они отстают по фазе соответственно от напряжений ![]() на угол, тангенс которого
на угол, тангенс которого![]() Из таблиц тригонометрических величин
Из таблиц тригонометрических величин ![]() .
.
Строим векторную диаграмму в масштабе: ![]() . Так как потенциал точки
. Так как потенциал точки ![]() равен потенциалу точки n (в фазе С тока нет), то разность потенциалов между точками С и n такая же, как и между точками
равен потенциалу точки n (в фазе С тока нет), то разность потенциалов между точками С и n такая же, как и между точками ![]() т.е. как между концами провода. Из векторной диаграммы следует, что это напряжение в 1,5 раза превышает номинальное фазное напряжение установки:
т.е. как между концами провода. Из векторной диаграммы следует, что это напряжение в 1,5 раза превышает номинальное фазное напряжение установки:![]() Если бы электромонтер стал сращивать концы провода (без отключения установки), он подвергся бы действию указанного напряжения.9. Три активных сопротивления:
Если бы электромонтер стал сращивать концы провода (без отключения установки), он подвергся бы действию указанного напряжения.9. Три активных сопротивления: ![]() — соединены звездой и присоединены к трехпроводной трехфазной линии с линейными напряжениями 120 В.
— соединены звездой и присоединены к трехпроводной трехфазной линии с линейными напряжениями 120 В.
Определить напряжения на отдельных сопротивлениях и токи в них.Решение:
Нагрузка фаз по условию задачи однородная (активная): ![]() . Однако симметричный режим в цепи невозможен, так как
. Однако симметричный режим в цепи невозможен, так как ![]() . В случае отсутствия нейтрального провода также невозможно обеспечить равенство напряжений на отдельных фазах при такой нагрузке.
. В случае отсутствия нейтрального провода также невозможно обеспечить равенство напряжений на отдельных фазах при такой нагрузке.
Изменение фазных напряжений при изменении нагрузки в одной фазе можно связать со смещением точки n на векторной диаграмме. При симметричном режиме в цепи точка n находится в центре тяжести треугольника линейных напряжений.
Допустим, что в линейном проводе С произошел разрыв, прекративший ток в этой фазе ![]() . В других фазах проходит ток при действии линейного напряжения
. В других фазах проходит ток при действии линейного напряжения ![]() в неразветвленной цепи, состоящей из сопротивлений
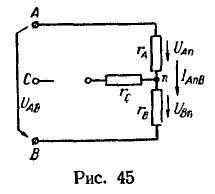
в неразветвленной цепи, состоящей из сопротивлений ![]() (рис. 45). Этот ток определяется по закону Ома:
(рис. 45). Этот ток определяется по закону Ома:![]()
При этом напряжение на сопротивлении ![]()
![]()
а напряжение на сопротивлении ![]()
![]()
Оба эти напряжения совпадают по фазе с током ![]() и, следовательно, с напряжением
и, следовательно, с напряжением ![]() (так как
(так как ![]() ).
).
Напряжения ![]() являются частями напряжения
являются частями напряжения ![]() , причем
, причем![]() Точка n, обозначенная в виде
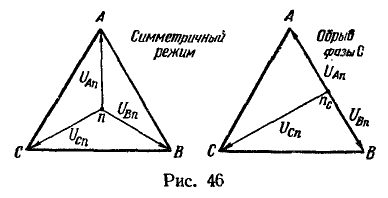
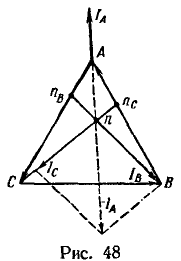
Точка n, обозначенная в виде ![]() , в случае обрыва фазы С находится на стороне АВ треугольника векторов линейных напряжений и делит ее в отношении 1:2 (рис. 48). Этот треугольник построен в масштабе
, в случае обрыва фазы С находится на стороне АВ треугольника векторов линейных напряжений и делит ее в отношении 1:2 (рис. 48). Этот треугольник построен в масштабе ![]() . Точку
. Точку ![]() , нанесенную на стороне AB, соединяем отрезком прямой с вершиной С, в которой располагается точка n при коротком замыкании фазы С
, нанесенную на стороне AB, соединяем отрезком прямой с вершиной С, в которой располагается точка n при коротком замыкании фазы С ![]() , когда потенциалы точек n и С равны.
, когда потенциалы точек n и С равны.
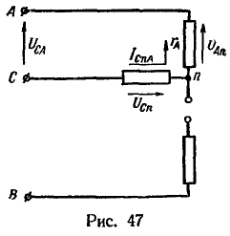
Допустим, что разрыв произошел в линейном проводе В (рис. 47). В этом случае ток ![]() , а в фазах С и А проходит один и тот же ток, равный, по закону Ома,
, а в фазах С и А проходит один и тот же ток, равный, по закону Ома,![]() Напряжения на участках неразветвленной цепи
Напряжения на участках неразветвленной цепи ![]() относятся, как сопротивления этих участков:
относятся, как сопротивления этих участков: ![]() ; кроме того, соблюдается равенство
; кроме того, соблюдается равенство ![]() . Следовательно, сторону СА следует разбить на части, относящиеся друг к другу как 3:1 (точка
. Следовательно, сторону СА следует разбить на части, относящиеся друг к другу как 3:1 (точка ![]() на рис. 48).
на рис. 48).
Соединяем отрезком прямой точку ![]() с точкой В, в которой располагается точка n при коротком замыкании фазы В. Прямые, проведенные внутри треугольника АВС, пересекаются в точке n; она соответствует узловой точке n электрической схемы для случая всех трех исправных проводов, так как точка пересечения этих прямых удовлетворяет обоим условиям, положенным в основу проведения прямых, т. е.
с точкой В, в которой располагается точка n при коротком замыкании фазы В. Прямые, проведенные внутри треугольника АВС, пересекаются в точке n; она соответствует узловой точке n электрической схемы для случая всех трех исправных проводов, так как точка пересечения этих прямых удовлетворяет обоим условиям, положенным в основу проведения прямых, т. е.![]()
Именно в таком соотношении находятся сопротивления фаз по условию задачи.
Теперь рассмотрим отрезки прямых, соединяющих точку n с точками А, В и С. На векторной диаграмме эти точки соответствуют потенциалам одноименных точек схемы, а отрезки прямых — напряжениям схемы. Отрезок An означает напряжение ![]() , отрезок Вn — соответственно напряжение
, отрезок Вn — соответственно напряжение ![]() , отрезок Сn — напряжение
, отрезок Сn — напряжение ![]() (в масштабе, принятом в начале построения
(в масштабе, принятом в начале построения ![]() ).
).
Путем измерения этих отрезков и применения масштаба устанавливаем, что ![]() .
.
Далее, зная сопротивления ![]() , определяем по закону Ома токи:
, определяем по закону Ома токи: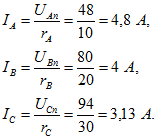 Эти токи совпадают по фазе соответственно с напряжениями
Эти токи совпадают по фазе соответственно с напряжениями ![]() , так как нагрузка активная.
, так как нагрузка активная.
Построим векторы токов в масштабе ![]() , направляя векторы токов вдоль векторов соответствующих напряжений. Сумма построенных векторов токов должна равняться нулю:
, направляя векторы токов вдоль векторов соответствующих напряжений. Сумма построенных векторов токов должна равняться нулю:![]() Несмотря на то что меньшее напряжение оказалось в фазе с меньшим сопротивлением (фаза А), ток в ней по сравнению с токами других фаз наибольший.
Несмотря на то что меньшее напряжение оказалось в фазе с меньшим сопротивлением (фаза А), ток в ней по сравнению с токами других фаз наибольший.
Смотри полное содержание по представленным решенным задачам.

